1.简介
1.1 应用背景
与云端的GPU设备相比,端侧的设备在成本和功耗方面具有明显优势。
但在端侧的设备具有更小的内存,更小的算力,这对移动端的模型带来了更高的要求,端测模型需要满足模型尺寸小、计算复杂度低、电池耗电量低、部署灵活等条件。
| 设备类型 | 设备名 | 显存/内存 | 浮点算力 |
|---|---|---|---|
| GPU | RTX 3080 | 10G | 29117 GFLOPS |
| GPU | RTX 2080 Ti | 11G | 16626 GFLOPS |
| 端侧设备 | 树莓派4B | 2G/4G/8G | 13.5 GFLOPS |
1.2 模型压缩和加速介绍
模型压缩和加速是两个不同的话题,压缩重点在于减少网络参数量,加速则侧重在降低计算复杂度、提升并行能力等。有时候压缩并不一定能带来加速的效果,有时候又是相辅相成的。
模型压缩和加速可以从多个角度来优化。
- 算法层压缩加速。这个维度主要在算法应用层,也是大多数算法工程师的工作范畴。主要包括结构优化(如矩阵分解、分组卷积、小卷积核等)、量化与定点化、模型剪枝、模型蒸馏等。
- 框架层加速。这个维度主要在算法框架层,比如tf-lite、NCNN、MNN等。主要包括编译优化、缓存优化、稀疏存储和计算、NEON指令应用、算子优化等
- 硬件层加速。这个维度主要在AI硬件芯片层,目前有GPU、FPGA、ASIC等多种方案,各种TPU、NPU就是ASIC这种方案,通过专门为深度学习进行芯片定制,大大加速模型运行速度。
本文将重点针对算法层压缩加速进行介绍。
2.算法层压缩加速
2.1 轻量架构设计/结构优化
2.1.1 分组卷积
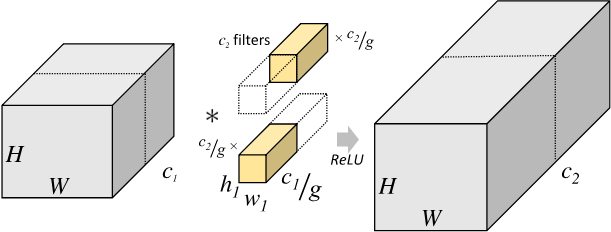
在分组卷积(Group convolution)中,输入特征图尺寸为 $H \times W \times c_1$,将输入特征图按照通道数分成 $g$组,则每组输入特征图的尺寸为$H \times W \times \frac{c_1}{g}$,对应的卷积核尺寸为 $h_1 \times w_1 \times \frac{c_1}{g}$ ,每组输出特征图尺寸为$H \times W \times \frac{c_2}{g}$,将$g$组结果拼接(concat),得到最终输出特征图尺寸为 $H \times W \times c_2$ ,因此分组卷积层的参数量为:
$$ h_1 \times w_1 \times \frac{c_1}{g} \times \frac{c_2}{g} \times g = h_1 \times w_1 \times c_1 \times c_2 \times \frac{1}{g} $$
即分组卷积的参数量是标准卷积的$\frac{1}{g}$。
2.1.2 MobileNet结构
MobileNetv1 论文
该论文最大的创新点是,提出了深度可分离卷积(depthwise separable convolution)。同时作者还使用了ReLU6激活函数来替代ReLU激活函数。
标准卷积
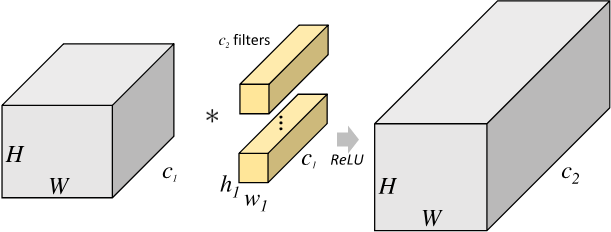
在标准卷积中,输入特征图尺寸为 $H \times W \times c_1$,卷积核尺寸为 $h_1 \times w_1 \times c_1$ ,输出特征图尺寸为 $H \times W \times c_2$ ,标准卷积层的参数量为:
$$ (h_1 \times w_1 \times c_1) \times c_2 $$
运算量约为(忽略偏置计算):
$$ w \times h \times c \times w_1 \times h_1 \times c_1 $$
深度可分离卷积
深度可分离卷(Depthwise separable convolution)积由逐通道卷积和逐点卷积两个部分组合而成,用来提取特征feature map。相比常规的卷积操作,其参数数量和运算成本比较低。
- 逐通道卷积
逐通道卷积(Depthwise Convolution)的一个卷积核负责一个通道,一个通道只被一个卷积核卷积。

该阶段等价于$g=c_1$的组卷积,其参数量为:
$$ h_1 \times w_1 \times 1 \times c_1 $$
计算量为:
$$ h_1 \times w_1 \times c_1 \times h_2 \times w_2 $$
- 逐点卷积
逐点卷积(Pointwise Convolution)的运算与常规卷积运算非常相似,它的卷积核的尺寸为 1×1×M,M为上一层的通道数。所以这里的卷积运算会将上一步的map在深度方向上进行加权组合,生成新的Feature map。有几个卷积核就有几个输出Feature map

该阶段按普通卷积的方式计算可得参数量为:
$$ 1 \times 1 \times c_1 \times c_2 $$
计算量为:
$$ h_2 \times w_2 \times c_1 \times c_2 $$
总参数量与计算量分析
则总的参数量为:$$ h_1 \times w_1 \times c_2 + c_1 \times c_2 $$
即深度可分离卷积的参数量是标准卷积的
$$ \frac{h_1 \times w_1 \times c_1 + c_1 \times c_2}{(h_1 \times w_1 \times c_1) \times c_2} = \frac{1}{c_2}+\frac{1}{h_1 \times w_1} $$
总的计算量为:
$$ h_1 \times w_1 \times c_1 \times h_2 \times w_2 +h_2 \times w_2 \times c_1 \times c_2 $$
即深度可分离卷积的的计算量是标准卷积的:
$$ \frac{h_1 \times w_1 \times c_1 \times h_2 \times w_2 +h_2 \times w_2 \times c_1 \times c_2}{h_1 \times w_1 \times c_1 \times h_2 \times w_2} = \frac{1}{c_2}+\frac{1}{h_1 \times w_1} $$
ReLU6
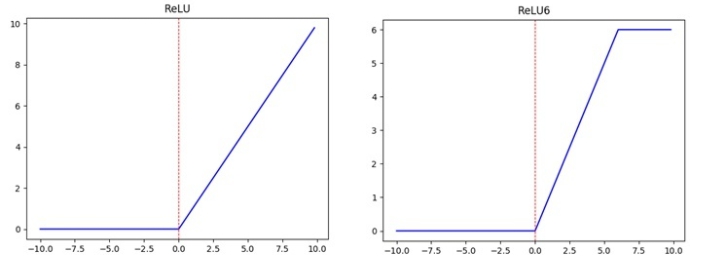
$$ ReLU = max(0,x) \\ ReLU6 = max(max(0,x),6) $$
上图左边是普通的ReLU,对于大于0的值不进行处理,右边是ReLU6,当输入的值大于6的时候,返回6,relu6“具有一个边界”。作者认为ReLU6作为非线性激活函数,在低精度计算下具有更强的鲁棒性。(这里所说的“低精度”,我看到有人说不是指的float16,而是指的定点运算(fixed-point arithmetic))
MobileNetv2 论文
有人在实际使用深度可分离卷积的时候, 发现深度卷积部分的卷积核比较容易训废掉:训完之后发现深度卷积训出来的卷积核有不少是空的(参数都为0了),作者认为这是ReLU激活函数的锅。
因此,作者将V2在V1的基础上,引入了Inverted Residuals(倒残差模块)和Linear Bottlenecks。
简单来说,就是当低维信息映射到高维,经过ReLU后再映射回低维时,若映射到的维度相对较高,则信息变换回去的损失较小;若映射到的维度相对较低,则信息变换回去后损失很大,如下图所示。

因此,作者认为对低维度做ReLU运算,很容易造成信息的丢失。而在高维度进行ReLU运算的话,信息的丢失则会很少。另外一种解释是,高维信息变换回低维信息时,相当于做了一次特征压缩,会损失一部分信息,而再进过ReLU后,损失的部分就更加大了。作者为了这个问题,就将ReLU替换成线性激活函数。
Inverted Residuals/倒残差模块
- 残差模块:输入首先经过$1 \times 1$的卷积进行压缩,然后使用$3 \times 3$的卷积进行特征提取,最后在用$1 \times 1$的卷积把通道数变换回去。整个过程是“压缩-卷积-扩张”。这样做的目的是减少$3 \times 3$模块的计算量,提高残差模块的计算效率。
- 倒残差模块:输入首先经过$1 \times 1$的卷积进行通道扩张,然后使用$3 \times 3$的depthwise卷积,最后使用$1 \times 1$的pointwise卷积将通道数压缩回去。整个过程是“扩张-卷积-压缩”。为什么这么做呢?因为depthwise卷积不能改变通道数,因此特征提取受限于输入的通道数,所以将通道数先提升上去。文中的扩展因子为6。
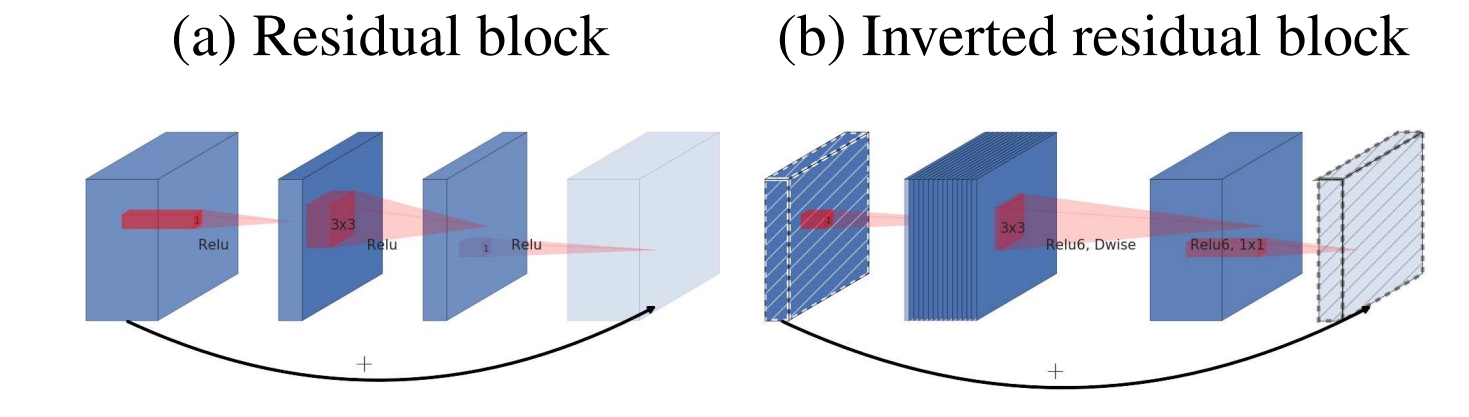
Linear Bottlenecks
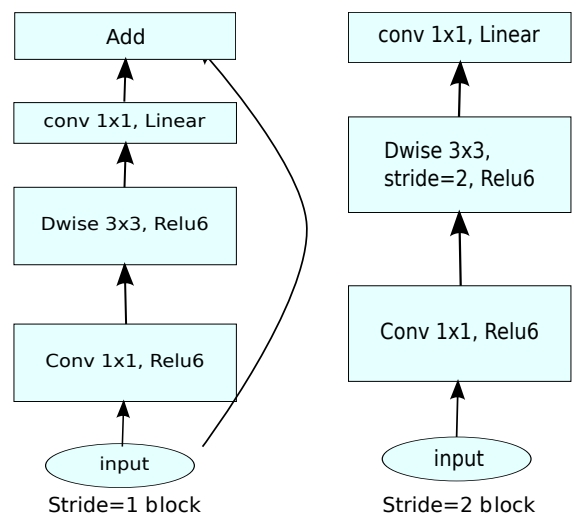
这个模块是为了解决上面提出的那个低维-高维-低维的问题,即将最后一层的ReLU替换成线性激活函数,而其他层的激活函数依然是ReLU6。如下图所示。当stride=1时,输入首先经过$1 \times 1$的卷积进行通道数的扩张,此时激活函数为ReLU6;然后经过$3 \times 3$的depthwise卷积,激活函数是ReLU6;接着经过$1 \times 1$的pointwise卷积,将通道数压缩回去,激活函数是linear;最后使用shortcut,将两者进行相加。而当stride=2时,由于input和output的特征图的尺寸不一致,所以就没有shortcut了。
MobileNetv3 论文
mobilenet V3并没有惊艳的结构提出,主要是一些tricks的应用和结合。v3版本结合了v1的深度可分离卷积、v2的Inverted Residuals和Linear Bottleneck、h-swish非线性变换、SE模块,利用NAS(神经结构搜索)来搜索网络的配置和参数。
引入SE结构
在bottlenet结构中加入了SE结构,并且放在了depthwise filter之后,如下图:

因为SE结构会消耗一定的时间,所以作者在含有SE的结构中,将expansion layer的channel变为原来的1/4,这样作者发现,即提高了精度,同时还没有增加时间消耗。
修改尾部结构
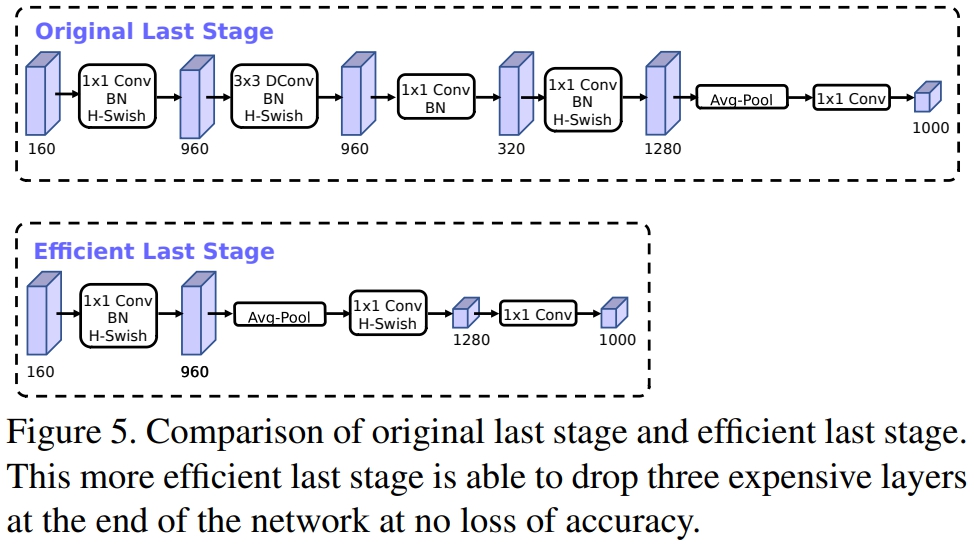
在mobilenetv2中,在avg pooling之前,存在一个$1 \times 1$的卷积层,目的是提高特征图的维度,更有利于结构的预测,但是这其实带来了一定的计算量了,所以这里作者修改了,将其放在avg pooling的后面,首先利用avg pooling将特征图大小由$7 \times 7$降到了$1 \times 1$,降到$1 \times 1$后,然后再利用$1 \times 1$提高维度,这样就减少了$7 \times 7=49$倍的计算量。
为了进一步的降低计算量,作者直接去掉了前面纺锤型卷积的$3 \times 3$以及$1 \times 1$卷积,进一步减少了计算量,就变成了如上图第二行所示的结构,作者将其中的$3 \times 3$以及$1 \times 1$去掉后,精度并没有得到损失。这里降低了大约15ms的速度。
修改channel数量
修改头部卷积核channel数量,mobilenet v2中使用的是$32 \times 3 \times 3$,作者发现,其实32可以再降低一点,所以这里作者改成了16,在保证了精度的前提下,降低了3ms的速度。
非线性变换(新激活函数)的改变
谷歌提出了一种新出的激活函数swish x(如下) 能有效改进网络精度,但是计算量太大了。
$$ swish(x)=x \cdot \sigma(x) = x \cdot sigmoid(x) $$
作者使用h-swish来近似替代sigmoid,进行了速度优化,具体如下:
$$ h-swish(x)=x \frac{ReLU6(x+3)}{6} $$
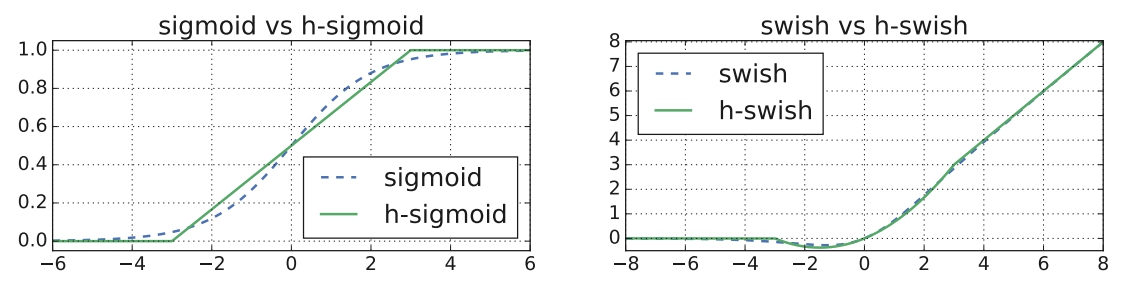
利用ReLU有几点好处:
1.可以在任何软硬件平台进行计算
2.量化的时候,它消除了潜在的精度损失,使用h-swish替换swish,在量化模式下回提高大约15%的效率,另外,h-swish在深层网络中更加明显。
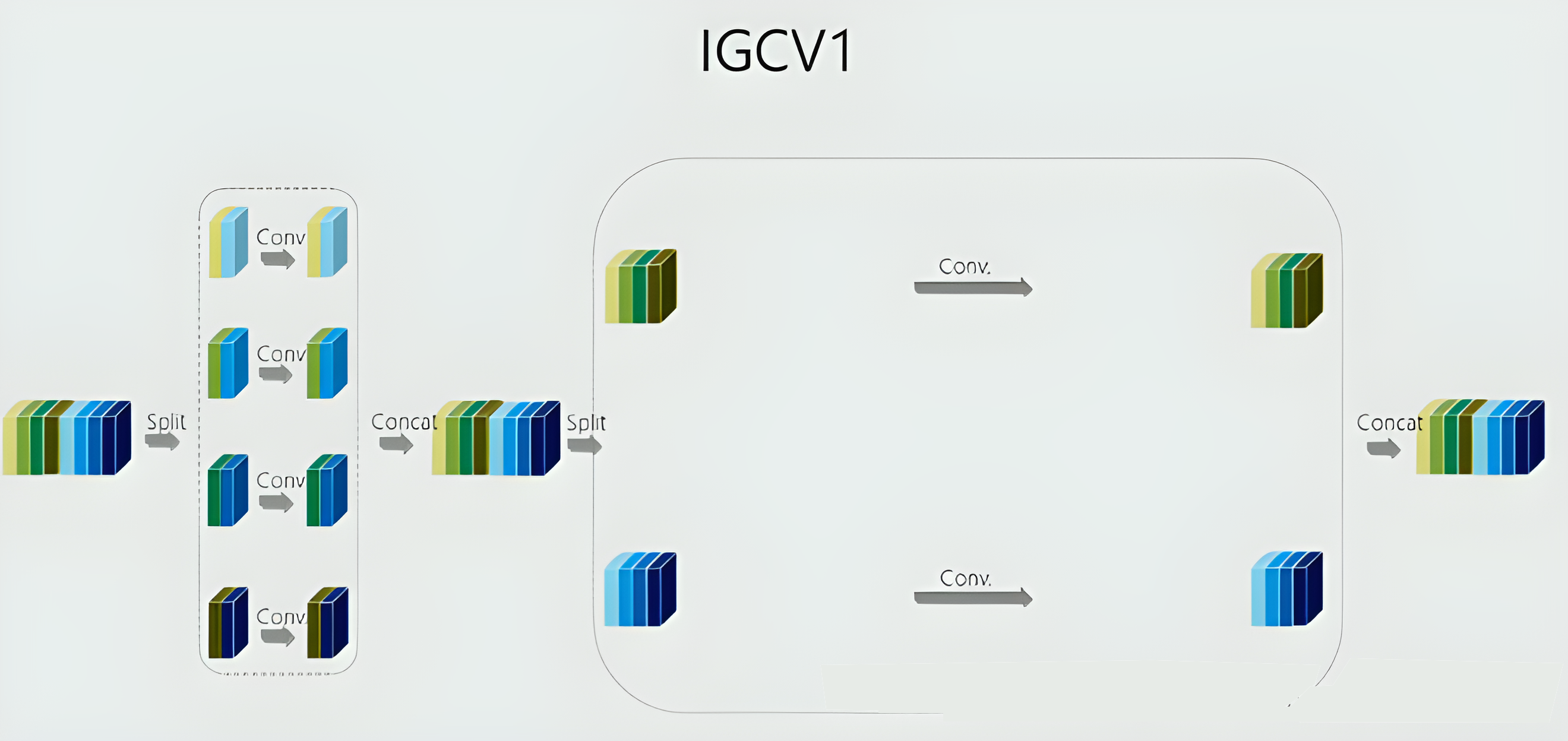
2.1.3 IGC结构
IGCv1 论文
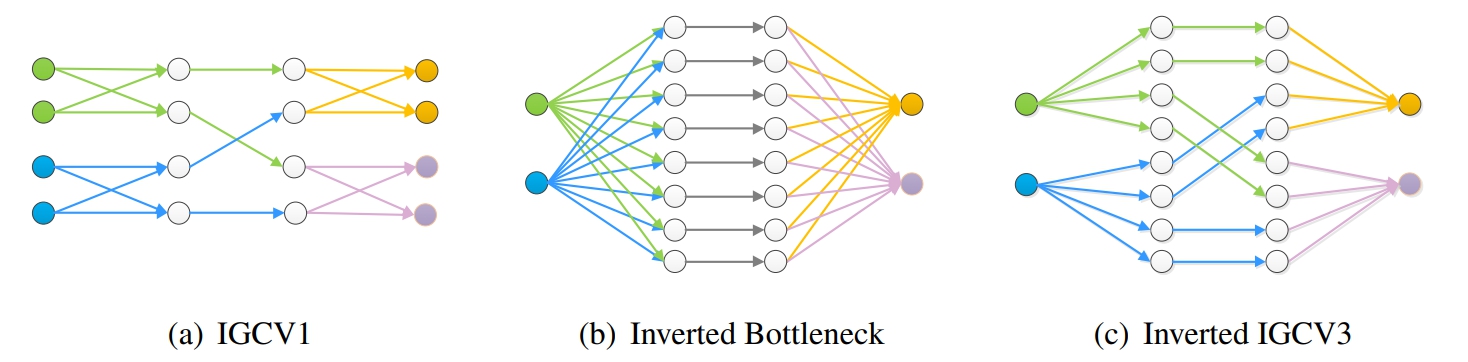
它的重点在于提出了一个新颖的构建块--交错组卷积。
交错组卷积
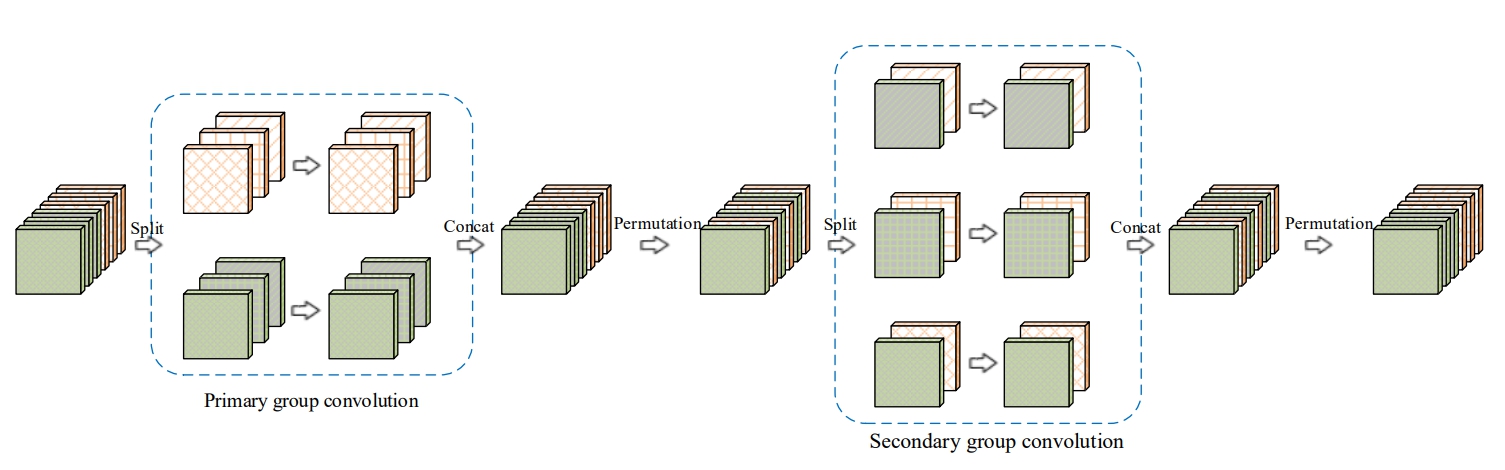
它是一种交错组卷积块的堆叠结构。每个块包含两个组卷积: 第一次组卷积核第二次组卷积,所谓组卷积就是在卷积时有两个分组。
- 第一次组卷积是把输入通道划分为L个组,每个组包含M个通道,然后将L个分组卷积的结果拼接在一起得到新的输入其仍然有LxM个通道之后打乱顺序
- 第二次组卷积划分了M个组,每个组包含L个通道,且这L个通道来自第一次分组卷积时的不同组。
- 同时第一次卷积做的是空间域卷积,第二次做的是逐点卷积。
比起普通卷积,在网络参数量和计算复杂度不变的同时,使得网络变得更宽了。
IGCv1 vs Xception
IGCV是第一个空间域的$3 \times 3$Group Conv,之后接第二个$1 \times 1$逐点卷积来融合通道信息,乍一看和Xception很像,可以说Xception就是IGCV的一种极端情况,Group数和Channel数相等的情况。
作者列举了$L=1$以及$M=1$的极端情况,也就对应着普通卷积以及Xception的极端组卷积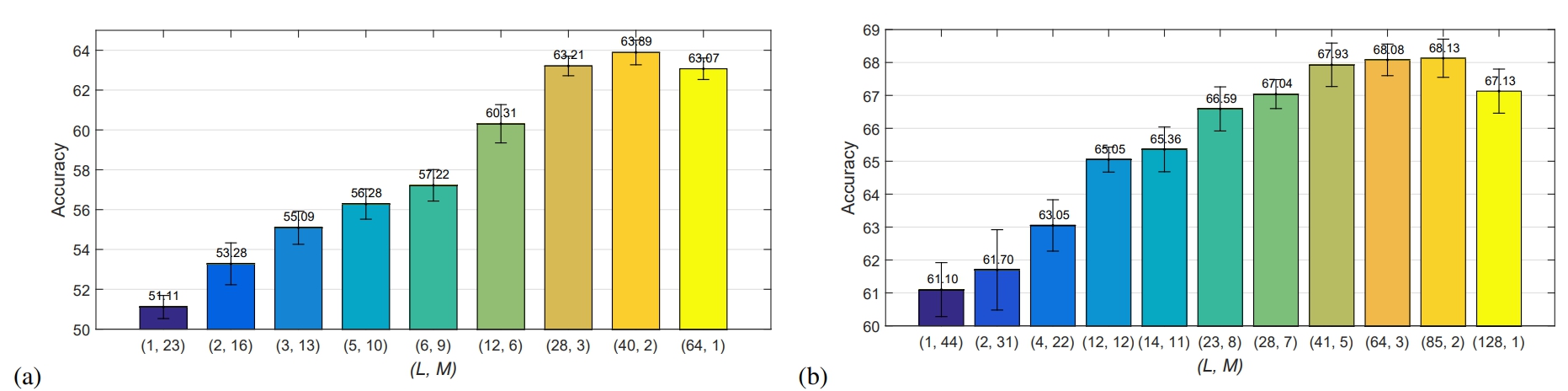
结果当然是IGCv1最好(摊手),从图上可以看到当每组只有2个通道的时候,效果是最好的,也就是文中最后IGCv1的结构了。
- 最后还补充了两次组卷积次序可以交换,并不影响结果;
- 可以将$3 \times 3$卷积分解成$3 \times 1$和$1 \times 3$,可以更加提高效率。
IGCv2 论文
IGCv2的主要创新点也就是在IGCv1的基础上,对于block里第二次组卷积再进行一次IGC。即使用多个稀疏卷积来替换原本比较稠密的卷积。
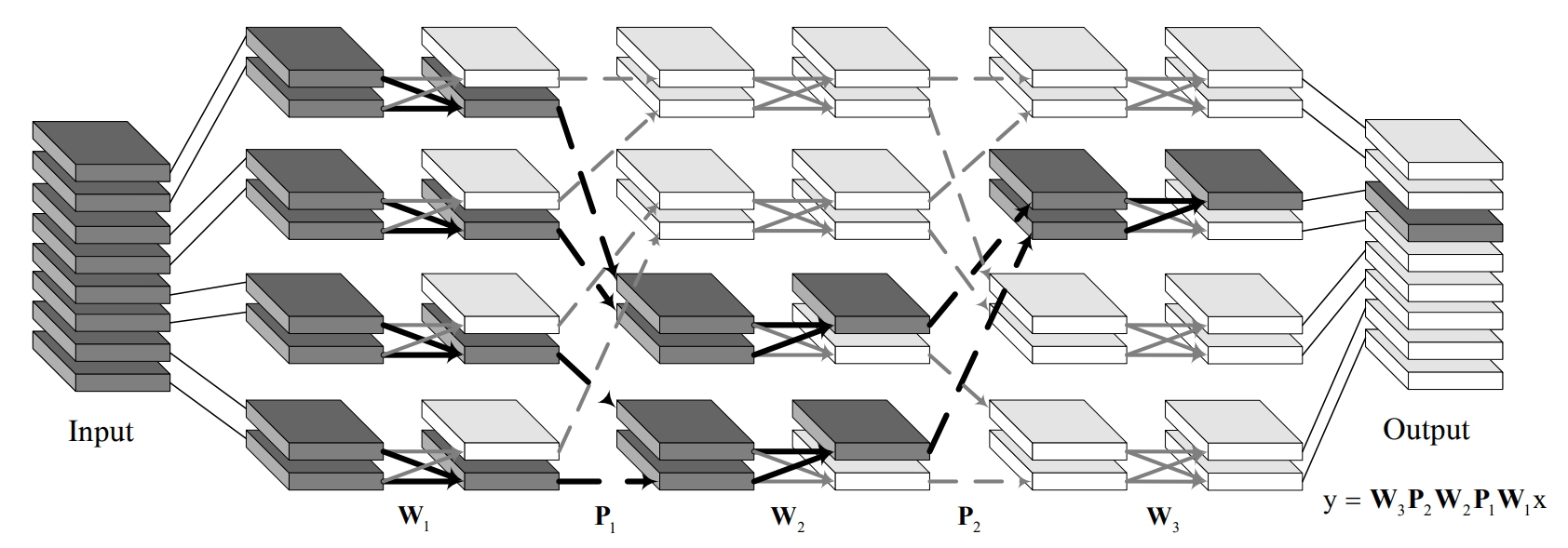
IGCv1 vs IGCv2
 IGCv1的结构如上图,可以看出第二次组卷积的时候,每一组的通道数仍然很多,文中的话就是比较dense, 因此想到对于每一组再进行IGC,这样就能进一步提升计算的效率了,也就是IGCv2,将每个组的普通卷积替换成交错组卷积,具体可见下图,
IGCv1的结构如上图,可以看出第二次组卷积的时候,每一组的通道数仍然很多,文中的话就是比较dense, 因此想到对于每一组再进行IGC,这样就能进一步提升计算的效率了,也就是IGCv2,将每个组的普通卷积替换成交错组卷积,具体可见下图,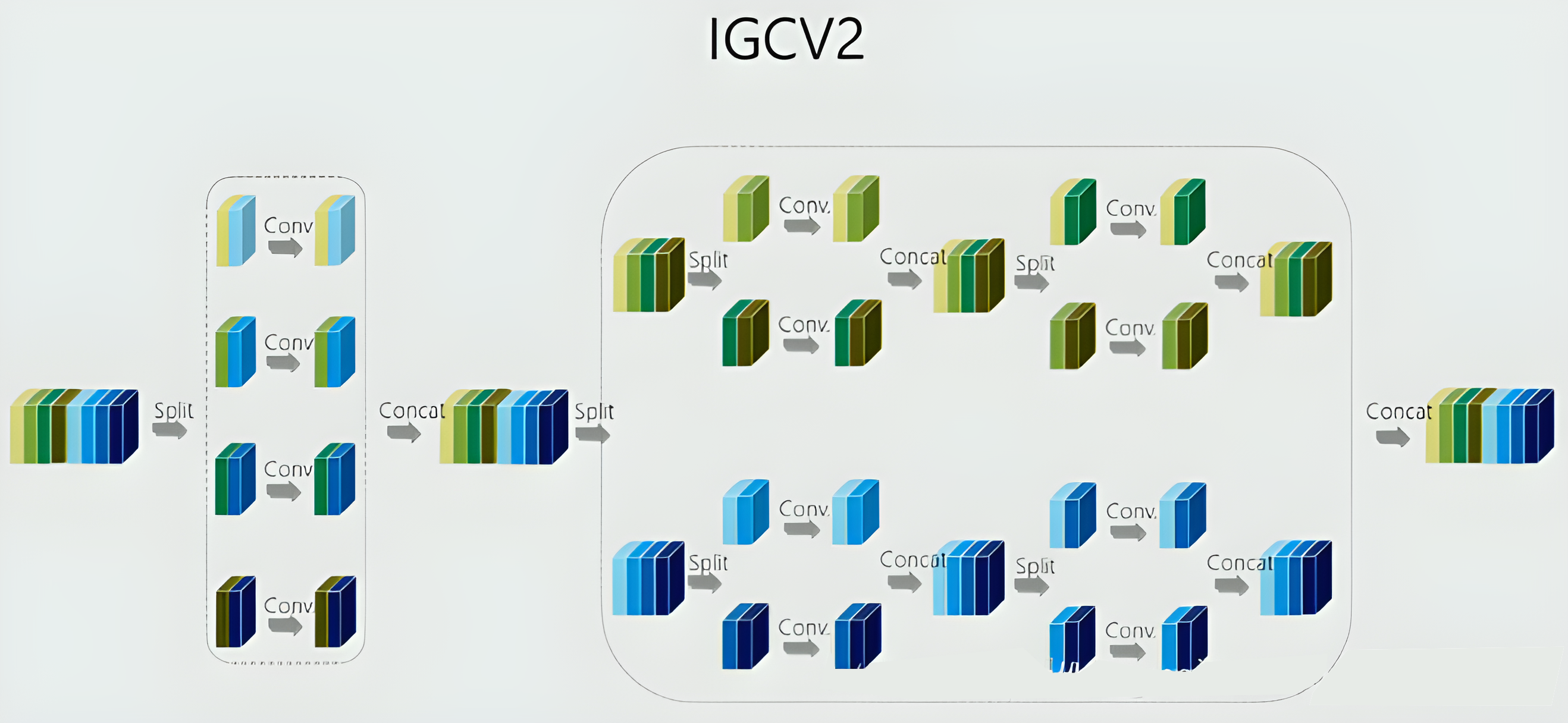
IGCv3 论文
IGCV3的主要创新点对IGCV2的结构进行延伸,引入低秩分组卷积来代替原本的分组卷积。就是先用1x1Group Pointwise Covolution升维,再3x3的组卷积,再通过1x1Group Pointwise Covolution进行降维,主要结构如下图
与MobileNetV2的对比,基本上就是1x1卷积改成了1x1的组卷积。
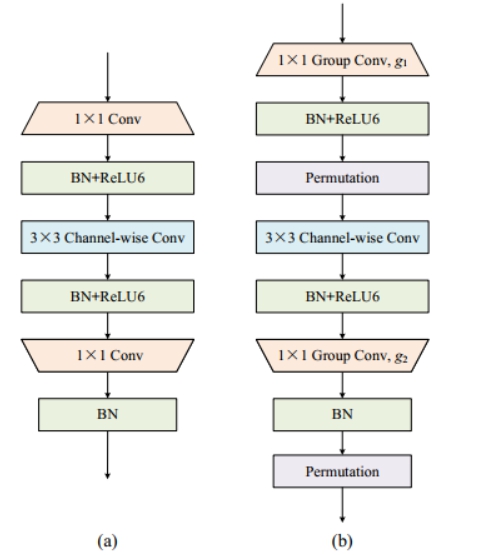
IGCV3在IGCV2的基础上融合了MobileNetV2的主要结构,并且使用更狠的低秩稀疏分组卷积,在整体结构上和MobileNetV2十分接近,核心依然是在稀疏分组卷积以及排序操作,虽然性能比MobileNetV2有些许提升,但整体的创新性略显不足。
2.1.4 Inception结构
Inception结构作用原理:Inception的作用就是替代了人工确定卷积层中过滤器的类型或者是否创建卷积层和池化层,让网络自己学习它具体需要什么参数。
Inception-v1 论文
提高网络最简单粗暴的方法就是提高网络的深度和宽度,即增加隐层和以及各层神经元数目。但这种简单粗暴的方法存在一些问题:
- 会导致更大的参数空间,更容易过拟合
- 需要更多的计算资源
- 网络越深,梯度容易消失,优化困难(这时还没有提出BN时,网络的优化极其困难)
Inception-v1的目标就是,提高网络计算资源的利用率,在计算量不变的情况下,提高网络的宽度和深度。

首先看第一个结构,有四个通道,有$1 \times 1、3 \times 3、5 \times 5$卷积核,该结构有几个特点:
- 采用大小不同的卷积核,意味着感受野的大小不同,就可以得到不同尺度的特征。
- 采用比较大的卷积核即$5 \times 5$,因为有些相关性可能隔的比较远,用大的卷积核才能学到此特征。
但是这个结构有个缺点,$5 \times 5$的卷积核的计算量太大。那么作者想到了第二个结构,用$1 \times 1$的卷积核进行降维。
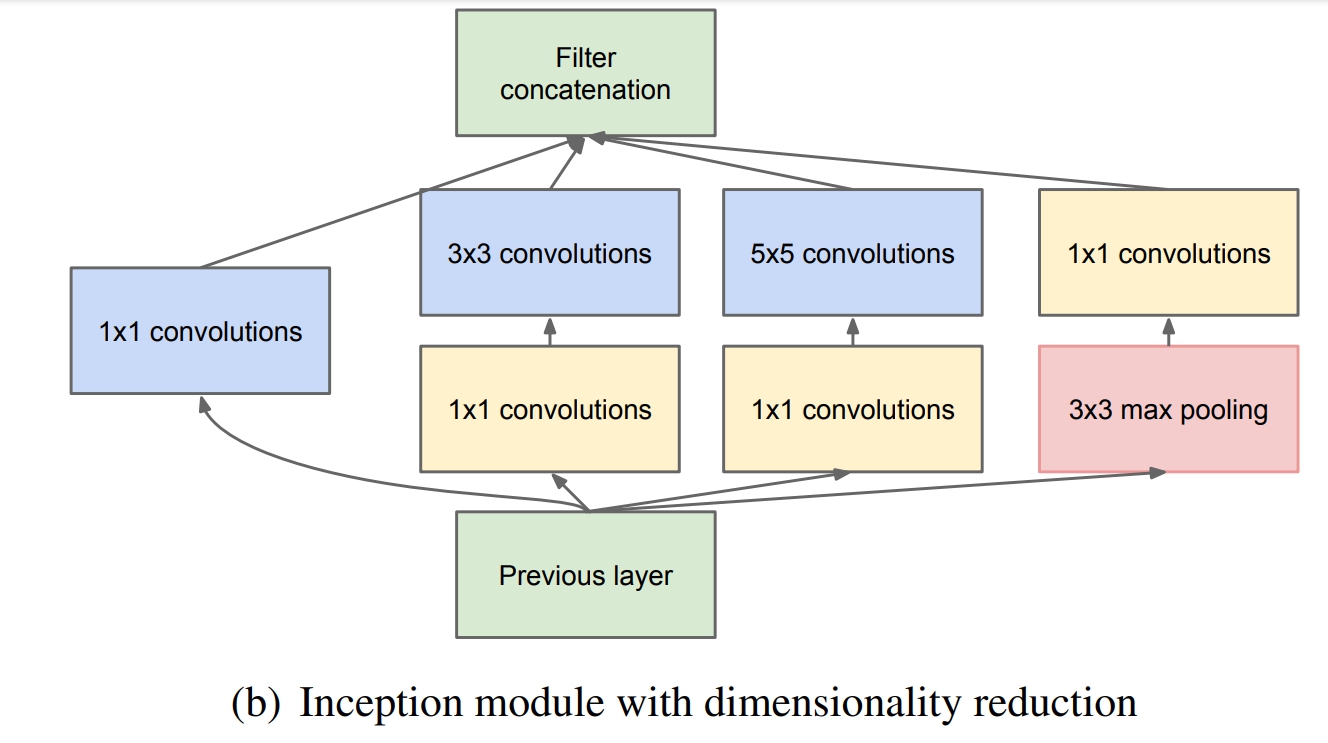
这个1*1的卷积核,它的作用就是:
- 降低维度,减少计算瓶颈
- 增加网络层数,提高网络的表达能力
那么在具体的卷积神经网络中,Inception应该放在哪里,作者的建议,在底层保持传统卷积不变,在高层使用Inception结构。
Inception-v2 论文
其主要思想在于提出了Batch Normalization,其次才是稍微改进了一下Inception,把Inception-v1中$5 \times 5$的卷积用2个$3 \times 3$的卷积替换。
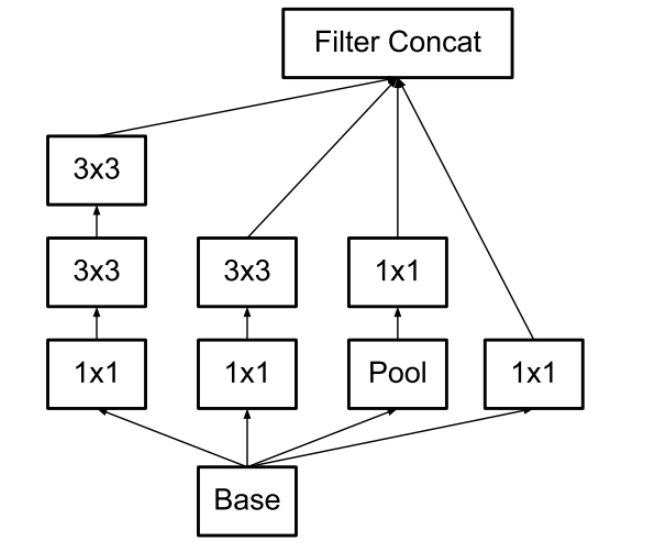
这样做法有两个优点:
- 保持相同感受野的同时减少参数
- 加强非线性的表达能力
Inception-v3 论文
主要从分解卷积核尺寸、使用辅助分类器、改变降低特征图尺寸的方式三个方面进行改进(使用辅助分类器与轻量化设计关系不大)。
分解卷积核尺寸
- 分解为对称的小的卷积核,(参考上面的Inception-v2)
- 分解为不对称的卷积核
分解为不对称的卷积核就是将$n \times n$的卷积核替换成 $1 \times n$ 和$n \times 1$ 的卷积核堆叠,计算量又会降低。
但是该方法在大维度的特征图上表现不好,在特征图12-20维度上表现好。
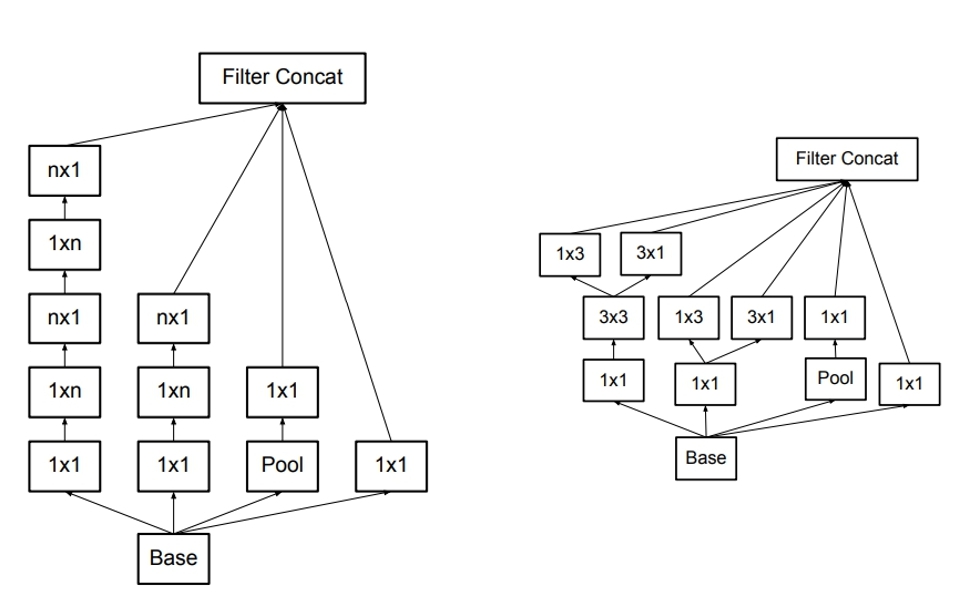
不对称分解方法有几个优点:
- 节约了大量的参数
- 增加一层非线性,提高模型的表达能力
- 可以处理更丰富的空间特征,增加特征的多样性
改变降低特征图尺寸的方式
在传统的卷积神经网络的中,当有pooling时(pooling层会大量的损失信息),会在之前增加特征图的厚度(就是双倍增加滤波器的个数),通过这种方式来保持网络的表达能力,但是计算量会大大增加。作者对传统的池化方式进行了如下的改进:
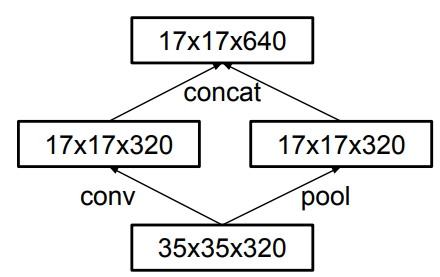
有两个通道,一个是卷积层,一个是pooling层,两个通道生成的特征图大小一样,concat在一起即可。
Inception-v4 [论文]()
本文的主要思想是将Inception与很火的ResNet结合,与轻量化设计的关系不大。
2.1.5 Xception结构
Xception 论文
Xception 是 Google 继 Inception 后提出的对 Inception-v3 的另一种改进。
作者认为,通道之间的相关性 与 空间相关性 最好要分开处理。采用 Separable Convolution(极致的 Inception 模块)来替换原来 Inception-v3中的卷积操作。
结构的变形过程如下:
- 在 Inception 中,特征可以通过$1 \times 1$卷积, $3 \times 3$卷积, $5 \times 5$ 卷积,pooling 等进行提取,Inception 结构将特征类型的选择留给网络自己训练,也就是将一个输入同时输给几种提取特征方式,然后做 concat 。Inception-v3的结构图如下:
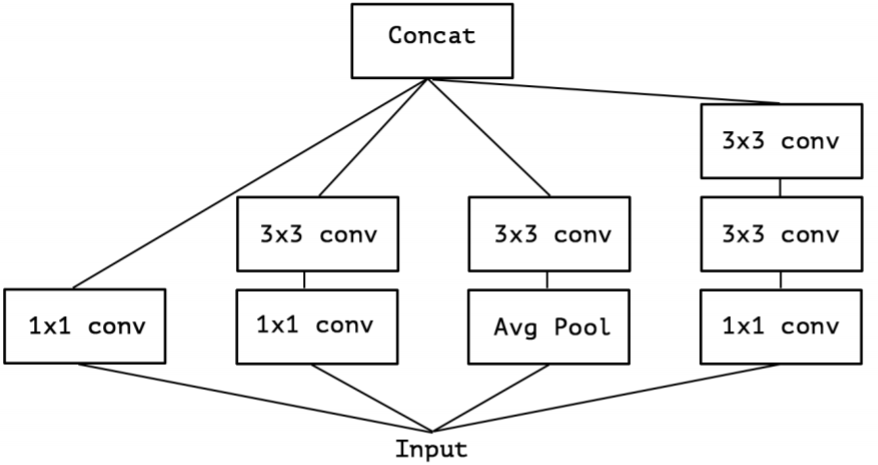
- 对 Inception-v3 进行简化,去除 Inception-v3 中的 avg pool 后,输入的下一步操作就都是 $1 \times 1$卷积:
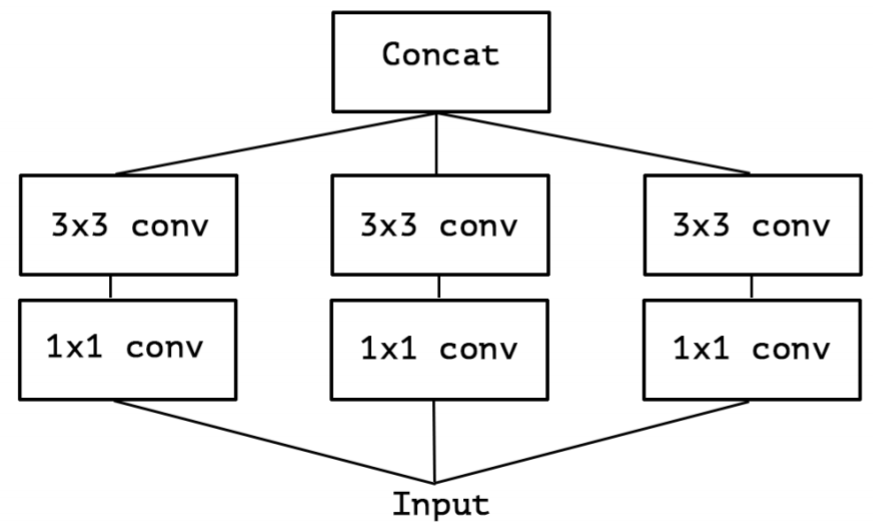
- 提取$1 \times 1$卷积的公共部分:

- Xception(极致的 Inception):先进行普通卷积操作,再对$1 \times 1$卷积后的每个channel分别进行$3 \times 3$卷积操作,最后将结果 concat:
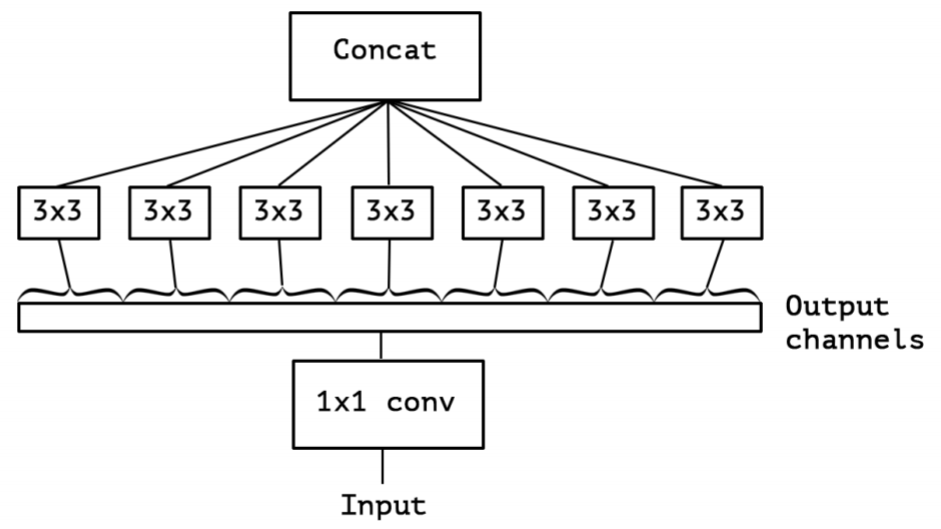
2.1.6 ResNeXt结构
ResNeXt 论文
ResNeXt是ResNet和Inception的结合体,不同于Inception v4的是,ResNext不需要人工设计复杂的Inception结构细节,而是每一个分支都采用相同的拓扑结构,ResNeXt的本质是分组卷积。
所有Inception模型都具有一个重要的性质——都是遵循 拆分-变换-合并(split-transform-merge) 的设计策略。Inception模型中block的输入会先被拆分成若干低维编码(使用$1 \times 1$卷积实现),然后经过多个不同的滤波器(如$3 \times 3$、$5 \times 5$等)进行转换,最后通过沿通道维度串联的方式合并。这种设计策略希望在保持网络计算复杂度相当低的前提下获取与包含大量且密集的层的网络具有相同的表示能力。
但是,Inception模型实现起来很麻烦,它包含一系列复杂的超参——每个变换的滤波器的尺寸和数量都需要指定,不同阶段的模块也需要定制。太多的超参数大多的影响因素,如何将Inception模型调整到适合不同的数据集/任务变得很不明晰。
简化Inception
基于此,作者的思想是每个结构使用相同的拓扑结构,那么这时候的Inception(这里简称简化Inception)表示为:
$$ y = \sum^{C}_{i=1}T_i(x) $$
其中 $C$ 是简Inception的基数(Cardinality),$T_i$是任意的变换,例如一系列的卷积操作等。Inception简化前后的对比如下图所示:
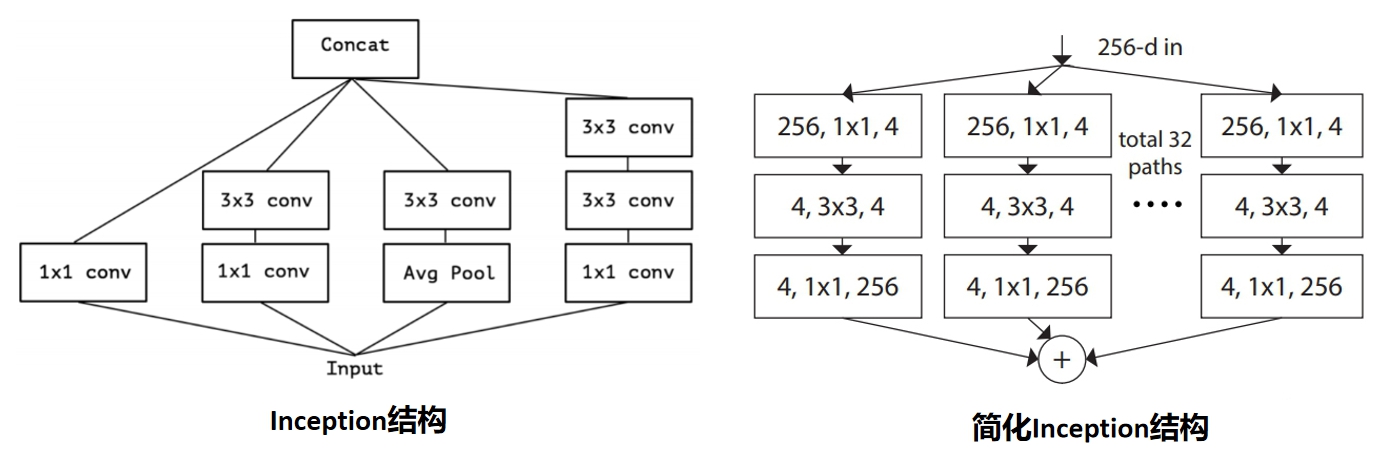
ResNeXt
再结合强大的残差网络,我们得到的便是完整的ResNeXt,也就是在简化Inception中添加一条short-cut,表示为:
$$ y = \sum^{C}_{i=1}T_i(x)+x $$
如下图所示:
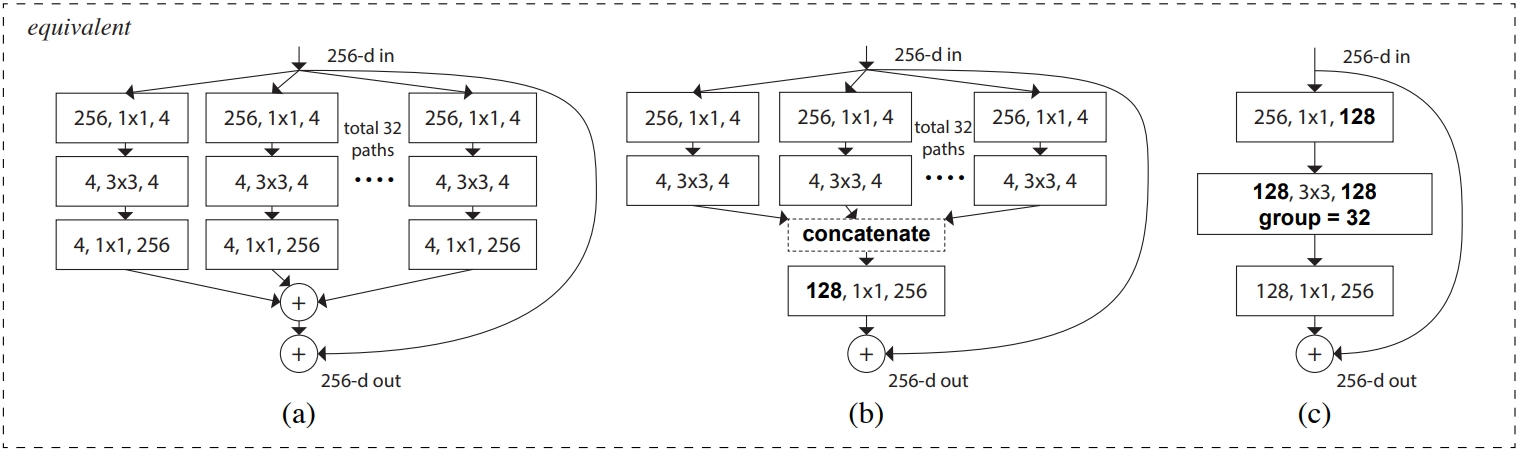
与Inception v4的区别
- ResNeXt的分支的拓扑结构是相同的,Inception V4需要人工设计;
- ResNeXt是先进行 $1 \times 1$卷积然后执行单位加,Inception V4是先拼接再执行 $1 \times 1$ 卷积。
2.1.7 ShuffleNet结构
ShuffleNet v1 [论文]()
作者通过分析Xception和ResNeXt模型,发现这两种结构通过卷积核拆分虽然计算复杂度均较原始卷积运算有所下降,然而拆分所产生的逐点卷积计算量却相当可观,成为了新的瓶颈。例如对于ResNeXt模型逐点卷积占据了93.4%的运算复杂度。可见,为了进一步提升模型的速度,就必须寻求更为高效的结构来取代逐点卷积。
受ResNeXt的启发,作者提出使用分组逐点卷积(group pointwise convolution)来代替原来的结构。通过将卷积运算的输入限制在每个组内,模型的计算量取得了显著的下降。然而这样做也带来了明显的问题:在多层逐点卷积堆叠时,模型的信息流被分割在各个组内,组与组之间没有信息交换(如图 1(a)所示)。这将可能影响到模型的表示能力和识别精度。
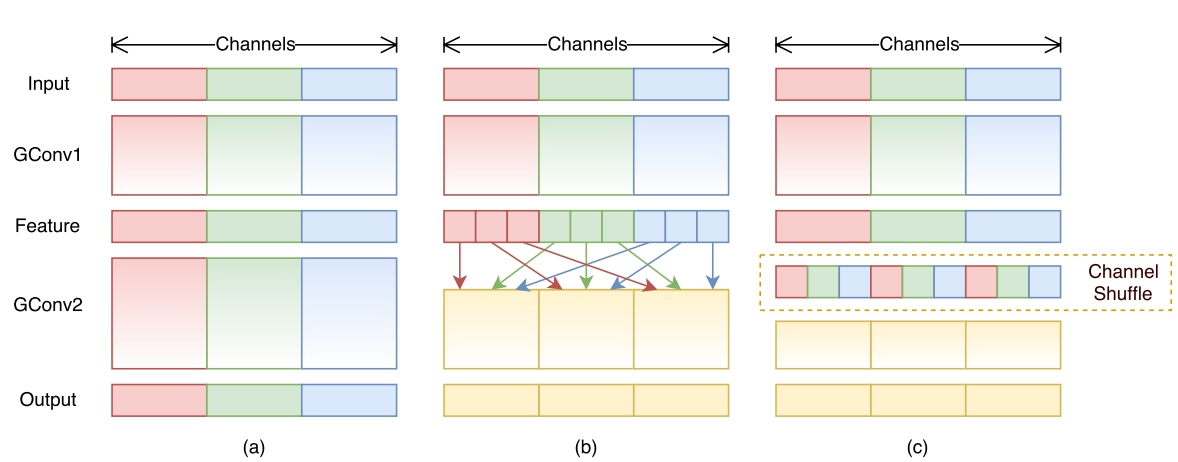
因此,在使用分组逐点卷积的同时,需要引入组间信息交换的机制。也就是说,对于第二层卷积而言,每个卷积核需要同时接收各组的特征作为输入,如上图(b)所示。作者指出,通过引入“通道重排”(channel shuffle,见上图(c))可以很方便地实现这一机制;并且由于通道重排操作是可导的,因此可以嵌在网络结构中实现端到端的学习。
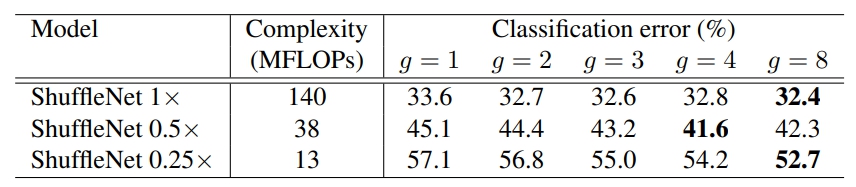
作者还观察到对于较小的网络(如ShuffleNet 0.25x),较大的分组会得到更好结果,认为更宽的通道对于小网络尤其重要。
ShuffleNet v2 论文
论文中提出了FLOPs不能作为衡量目标检测模型运行速度的标准,因为MAC(Memory access cost)也是影响模型运行速度的一大因素。
由此,作者通过实验得出4个设计小模型的准则:
- 卷积操作时,输入输出采用相同通道数可以降低MAC
- 过多的组,会导致MAC增加
- 分支数量过少,模型速度越快
- element-wise操作导致速度的消耗,远比FLOPs上体现的多。
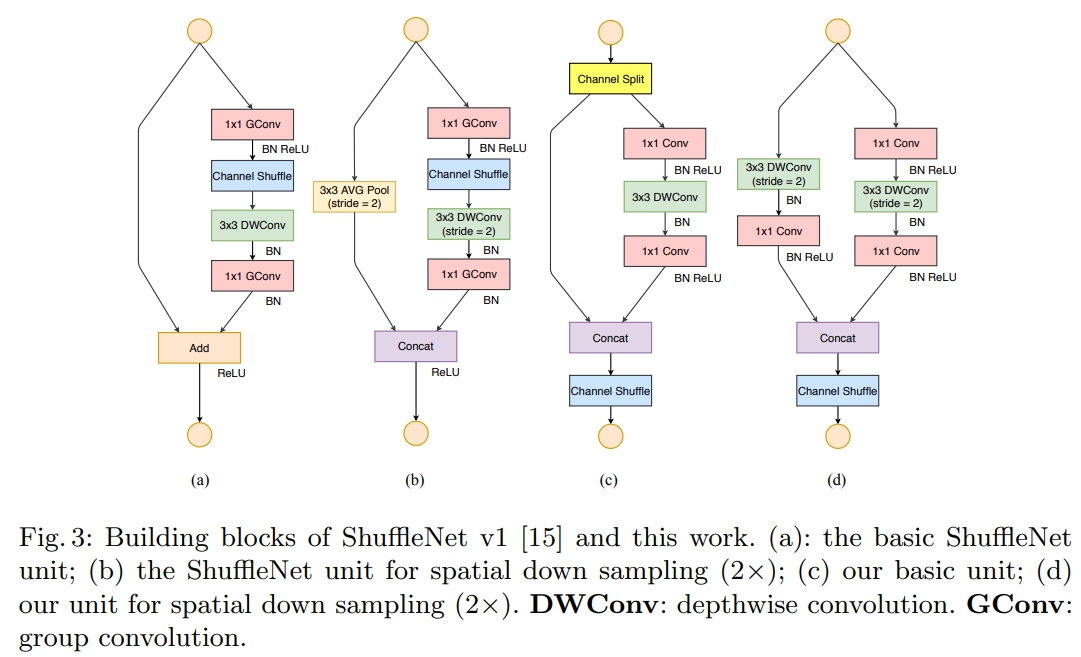
根据以上四点准则,作者在shuffleNet V1的基础上提出了修改得到了shuffleNet V2的基本快。
2.1.8 GhostNet结构
GhostNet 论文
作者通过对比分析ResNet-50网络第一个残差组(Residual group)输出的特征图可视化结果,发现一些特征图高度相似(如Ghost一般,下图中的三组box内的图像对)。

如果按照传统的思考方式,可能认为这些相似的特征图存在冗余,是多余信息,想办法避免产生这些高度相似的特征图。但本文思路清奇,推测CNN的强大特征提取能力和这些相似的特征图(Ghost对)正相关,不去刻意的避免产生这种Ghost对,而是尝试利用简单的线性操作来获得更多的Ghost对。
常规卷积
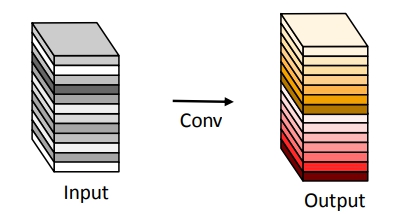
输入为$Y = w \times h \times c$,输出为$Y_1 = w_1 \times h_1 \times c_1$,运算量约为$w \times h \times c \times w_1 \times h_1 \times c_1$(忽略偏置计算)。
Ghost Module
Ghost Module分为常规卷积、Ghost生成和特征图拼接三步
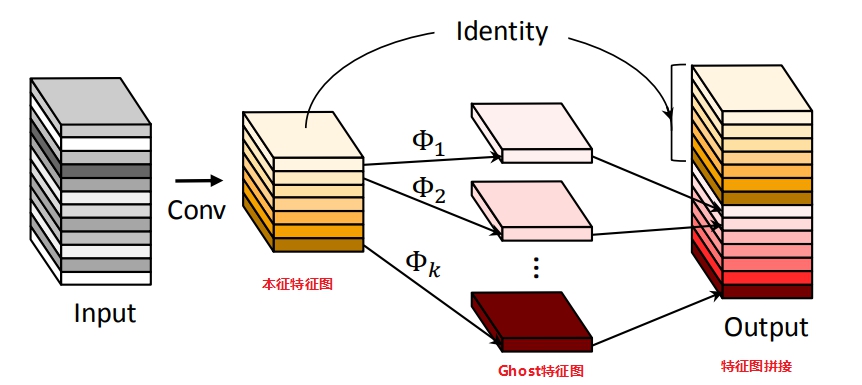
1.首先用常规卷积得到本征特征图$Y'$(intrinsic feature maps),
2.然后将本征特征图$Y'$每一个通道的特征图$y_i'$,用$\Phi_{i,j}$操作来产生Ghost特征图$y_{i,j}$
对线性操作 $\Phi_{i,j}$的理解:论文中表示,可以探索仿射变换和小波变换等其他低成本的线性运算来构建Ghost模块。但是,卷积是当前硬件已经很好支持的高效运算,它可以涵盖许多广泛使用的线性运算,例如平滑、模糊等。 此外,线性运算 $\Phi_{i,j}$的滤波器的大小不一致将降低计算单元(例如CPU和GPU)的效率,所以论文中实验中让Ghost模块中的滤波器size取固定值,并利用Depthwise卷积实现 $\Phi_{i,j}$ ,以构建高效的深度神经网络。
所以说,论文中使用的线性操作并不是常见的旋转、平移、仿射变换、小波变换等,而是用的Depthwise卷积。一种猜测可能是传统的线性操作效果没有Depthwise效果好,毕竟CNN可以自动调整filter的权值。
3.最后将第一步得到的本征特征图和第二步得到的Ghost特征图拼接(identity连接)得到最终结果OutPut。
当然也可以认为(论文中的思路),第2步中的$\Phi_{i,j}$中包含一个恒等映射,即将本征特征图直接输出,则不需用第三部,
例如:对于$Y’$中的每一个特征图,对其进行$s$次映射,$s$次中包含一次恒等映射,其余$s-1$次为cheap operate来得到Ghost特征图,最终得到输出结果,这二者理论上完全一致。
因此可以看出,Ghost Module和深度分离卷积是很类似的,不同之处在于先进行PointwiseConv,后进行DepthwiseConv,另外增加了DepthwiseConv的数量,包括一个恒定映射。
2.1.9 SENet结构
该结构与轻量化的关系不大,但是与提升整体的网络性能有关系,因此也放在这里一起进行介绍。
SENet 论文
SENet网络的创新点在于关注channel之间的关系,希望模型可以自动学习到不同channel特征的重要程度。论文通过显式地建模通道之间的相互依赖关系,自适应地重新校准通道的特征响应,从而设计了SE block如下图所示。论文的核心就是Squeeze和Excitation(论文牛的地方)两个操作。
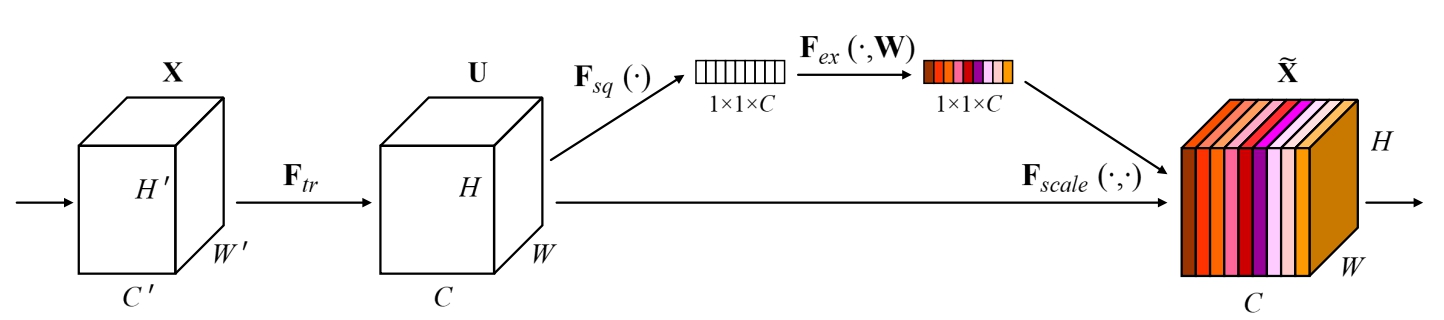
Squeeze(挤压)
由于卷积只是在一个局部空间内进行操作,$U$(特征图)很难获得足够的信息来提取channel之间的关系,对于网络中前面的层这更严重,因为感受野比较小。为了,SENet提出Squeeze操作,将一个channel上整个空间特征编码为一个全局特征,采用global average pooling来实现(原则上也可以采用更复杂的聚合策略):
$$ z_c = F_{sq}(u_c)=\frac{1}{H \times W}\sum^{H}_{i=1}\sum^{W}_{j=1}u_c(i,j),z \in R^C $$
Excitation(激励)
Sequeeze操作得到了全局描述特征,然后使用Excitation来抓取channel之间的关系。这个操作需要满足两个准则:首先要灵活,它要可以学习到各个channel之间的非线性关系;第二点是学习的关系不是互斥的,因为这里允许多channel特征,而不是one-hot形式。基于此,这里采用sigmoid形式的gating机制:
$$ s =F_{ex}(z,W)=\sigma(g(z,W))=\sigma(W_2ReLU(W_1z)) $$
为了降低模型复杂度以及提升泛化能力,这里采用包含两个全连接层的bottleneck结构,其中第一个FC层起到降维的作用,降维系数为r是个超参数,然后采用ReLU激活。最后的FC层恢复原始的维度。最后将学习到的各个channel的激活值(sigmoid激活,值0~1)乘以U上的原始特征(具体见下图SE模块在Inception和ResNet上的应用):
$$ \tildec=Fscale(u_c,s_c)=s_c \cdot u_c $$
整个操作可以看成学习到了各个channel的权重系数,从而使得模型对各个channel的特征更有辨别能力,这应该也算一种attention机制。
SE模块在Inception和ResNet上的应用

2.2 模型量化
模型:特指卷积神经网络(用于提取图像/视频视觉特征)
量化:将信号的连续取值(或者大量可能的离散取值)近似为有限多个(或较少的)离散值的过程。
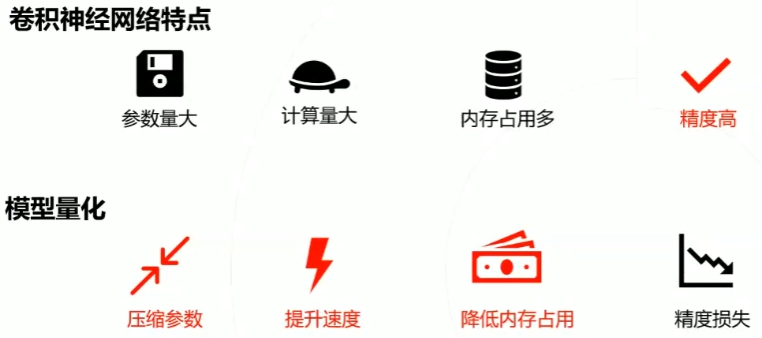
深度学习模型参数通常是32bit浮点型,我们能否使用16bit,8bit,甚至2bit来存储呢?答案是肯定的。这就是模型量化需要解决的问题。
是什么阻碍了量化模型的落地?
精度挑战大
- 线性量化对分布的描述不精确
- 8bit to 1bit:比特数越低,精度损失越大
- 分类to检测to识别:任务越难,精度损失越大
- 大模型to小模型:通常认为模型越小,精度损失越大
- Depthwise对量化不友好
- Merge BN, Fully Quantized
软硬件支持程度
- 不同硬件高效支持的低比特指令不一样
- 不同软件库提供的量化方案/量化细节不一样
- 不同软件库对于不同Layer的量化位置不一样
速度能否变快
- 不是所有的硬件上都提供高效的量化计算指令
- 针对体系结构精细的优化
- 不同结构优化方案不同
- 系统&算法协同设计
2.2.1 伪量化
所谓伪量化是指在存储时使用低精度进行量化,但推理时会还原为正常高精度。
为什么推理时不仍然使用低精度呢?这是因为一方面框架层有些算子只支持浮点运算,需要专门实现算子定点化才行。另一方面,高精度推理准确率相对高一些。伪量化可以实现模型压缩,但对模型加速没有多大效果。
普通伪量化
常见的做法是保存模型每一层时,利用低精度来保存每一个网络参数,同时保存拉伸比例scale(标度)和零值对应的浮点数zero_point(零点位置),量化公式如下:
$$ Q(input,scale,zero\_point) = round(\frac{input}{scale}+zero\_point) $$
推理阶段,再利用公式:
$$ input = zero\_point + Q(input,scale,zero\_point) \times scale $$
将网络参数还原为32bit浮点。
eg:假设量化为qint8,设量化后的数Q为00011101,scale = 0.025 , zero_point = 0;
最高位为0(符号位),所以是正数;后7位转换为10进制是29,所以Q代表的数为 :zero_point + Q scale = 0 + 29 0.025 = 0.725
聚类与伪量化
利用k-means等聚类算法,步骤如下:
- 将大小相近的参数聚在一起,分为一类。
- 每一类计算参数的平均值,作为它们量化后对应的值。
- 每一类参数存储时,只存储它们的聚类索引。索引和真实值(也就是类内平均值)保存在另外一张表中
- 推理时,利用索引和映射表,恢复为真实值。
过程如下图所示,
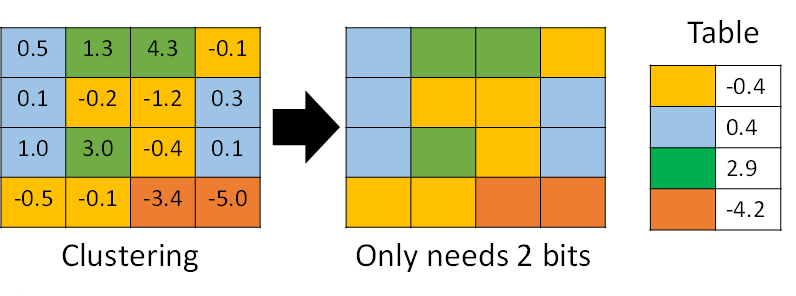
从上可见,当只需要4个类时,我们仅需要2bit就可以实现每个参数的存储了,压缩量达到16倍。推理时通过查找表恢复为浮点值,精度损失可控。
2.2.2 定点化
与伪量化不同的是,定点化在推理时,不需要还原为浮点数。这需要框架实现算子的定点化运算支持。目前NCNN、MNN、XNN等移动端AI框架中,均加入了定点化支持。
2.2.3 其他角度分类
二值化
$$ Q_B(x)=sgn(x)=\begin{cases} +1,& if \ x \ge 0 \\ -1,& otherwise \end{cases} $$
线性量化(对称、非对称、Ristretto)
Quantize
$$ x_{int} = round(\frac{\Delta})+z \\ x_Q = clamp(0,N_{levels}-1,x_{int}) $$
De-quantize
$$ x_{float}=(x_Q-z)\Delta $$
对数量化
- 可将乘法转变为加法,加法转变为索引
2.3 剪枝
TODO
参考资料
- 理解分组卷积和深度可分离卷积如何降低参数量
- 深度可分离卷积
- inception-v1,v2,v3,v4----论文笔记
- 深度学习模型轻量化(上)
- ShuffleNet:一种极高效的移动端卷积神经网络
- shuffleNet v1 v2笔记
- Xception
- ResNeXt详解
- ResNet系] 003 ResNeXt
- 最后一届ImageNet冠军模型:SENet
- GhostNet论文解析:Ghost Module
- MobileNet系列
- 轻量级神经网络“巡礼”(二)—— MobileNet,从V1到V3
- 轻量化网络:MobileNet v3解析
- mobilenet系列之又一新成员---mobilenet-v3
- 深度学习: 激活函数 (Activation Functions)
- 轻量级网络:IGCV系列V1、V2、V3
- IGC系列:全分组卷积网络,分组卷积极致使用 | 轻量级网络
- pytorch量化中torch.quantize_per_tensor()函数参数详解
- 深度学习模型轻量化(下)
- Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2015: 1-9.
- Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift[C]//International conference on machine learning. PMLR, 2015: 448-456.
- Szegedy C, Vanhoucke V, Ioffe S, et al. Rethinking the inception architecture for computer vision[C]//Proceedings of the IEEE conference on computer vision and pattern recognition. 2016: 2818-2826.
- Szegedy C, Ioffe S, Vanhoucke V, et al. Inception-v4, inception-resnet and the impact of residual connections on learning[C]//Thirty-first AAAI conference on artificial intelligence. 2017.
- 模型量化了解一下?
- 【商汤泰坦公开课】模型量化的那些事

评论 (0)