搜索到
6
篇与
的结果
-
TensorBoard:训练日志及网络结构可视化工具 1.安装pip install tensorboard2.可视化标量数据(loss和accuracy)from torch.utils.tensorboard import SummaryWriter import random # 实例化TensorBoard logs_writer = SummaryWriter('./logs') # 可视化标量数据 for epoch_id in range(100): logs_writer.add_scalar("train/loss",random.random(),epoch_id) logs_writer.add_scalar("train/accuracy",random.random(),epoch_id) logs_writer.add_scalar("test/loss",random.random(),epoch_id) logs_writer.add_scalar("test/accuracy",random.random(),epoch_id)tensorboard --logdir=logs --bind_all3.可视化网络结构""" 可视化网络结构 """ import torch import torch.nn as nn from torch.utils.tensorboard import SummaryWriter # 实例化TensorBoard writer = SummaryWriter('./model_vis') # 构建网络模型 - 使用自定义类 class Digit_Rec(nn.Module): def __init__(self): super(Digit_Rec,self).__init__() self.conv1 = nn.Conv2d(1,10,5) #1：灰度图片的通道，10：输出通道，5：kernel self.relu1 = nn.ReLU() self.max_pool = nn.MaxPool2d(2,2) self.conv2 = nn.Conv2d(10,20,3) #10：输入通道，20：输出通道，3：Kernel self.relu2 = nn.ReLU() self.fc1 = nn.Linear(20*10*10,500) # 20*10*10：输入通道，500：输出通道 self.relu3 = nn.ReLU() self.fc2 = nn.Linear(500,10) # 500：输入通道，10：输出通道 self.relu4 = nn.ReLU() self.softmax = nn.Softmax(dim=1) def forward(self,x): batch_size = x.size(0) # x的格式：batch_size x 1 x 28 x 28 拿到了batch_size x = self.conv1(x) # 输入：batch*1*28*28 输出：batch*10*24*24 x = self.relu1(x) x = self.max_pool(x) # 输入：batch*10*24*24输出：batch*10*12*12 x = self.conv2(x) x = self.relu2(x) x = x.view(batch_size,-1) #fatten 展平 -1自动计算维度，20*10*10=2000 x = self.fc1(x) # 输入：batch*2000 输出：batch*500 x = self.relu3(x) x = self.fc2(x) # 输入：batch*500 输出：batch*10 x = self.relu4(x) output = self.softmax(x) # 计算分类后，每个数字的概率值 return output model = Digit_Rec() model = Digit_Rec() images = torch.randn(1, 1, 28, 28) writer.add_graph(model, images) writer.close()tensorboard --logdir=model_vis --bind_all参考资料Pytorch中使用tensorboard学习笔记(2)记录损失loss和准确率accuracypytorch中使用tensorboard绘制Accuracy/Loss曲线（train和test显示在同一幅图中）pytorch中使用TensorBoard进行可视化Loss及特征图 -
VOC数据集的Anchor聚类--Kmeans算法实现 1.K-means算法具体介绍参考:Kmeans算法简介k-means聚类的算法运行过程：（1）选择k个初始聚类中心 （2）计算每个对象与这k个中心各自的距离，按照最小距离原则分配到最邻近聚类 （3）使用每个聚类中的样本均值作为新的聚类中心 （4）重复步骤（2）和（3）直到聚类中心不再变化 （5）结束，得到k个聚类2.算法实现2.1数据加载函数封装# STEP1:加载数据集，获取所有box的width、height import os from progressbar import * import xmltodict import numpy as np def load_dataset(data_root): xml_dir= os.path.join(data_root,"Annotations") #xml文件路径(Annotations) width_height_list = [] #用于存储统计结果 #进度条功能 widgets = ['box width_height 统计: ',Percentage(), ' ', Bar('#'),' ', Timer(),' ', ETA()] pbar = ProgressBar(widgets=widgets, maxval=len(os.listdir(xml_dir))).start() count = 0 for xml_file in os.listdir(xml_dir): # 拼接xml文件的path xml_file_path = os.path.join(xml_dir,xml_file) # 读取xml文件到字符串 with open(xml_file_path) as f: xml_str = f.read() # xml字符串转为字典 xml_dic = xmltodict.parse(xml_str) # 获取图片的width、height img_width = float(xml_dic["annotation"]["size"]["width"]) img_height = float(xml_dic["annotation"]["size"]["height"]) # 获取xml文件中的所有objects obj_list = [] objects = xml_dic["annotation"]["object"] if isinstance(objects,list): # xml文件中包含多个object for obj in objects: obj_list.append(obj) else: # xml文件中包含1个object obj_list.append(objects) #print(obj_list) # width_height布统计 for obj in obj_list: #box 的height\width归一化 box_width = (float(obj['bndbox']["xmax"]) - float(obj['bndbox']["xmin"]))/img_width box_height = (float(obj['bndbox']["ymax"]) - float(obj['bndbox']["ymin"]))/img_height width_height_list.append([box_width,box_height]) #更新进度条 count += 1 pbar.update(count) #释放进度条 pbar.finish()调用效果#输出统计结果信息 data_root = "/data/jupiter/project/dataset/209_VOC_new" width_height_list = load_dataset(data_root) width_height_np = np.array(width_height_list) print("clustering feature data is ready. shape = (N object, width and height) = {}".format(width_height_np.shape))box width_height 统计: 100% |###############| Elapsed Time: 0:00:35 Time: 0:00:35 clustering feature data is ready. shape = (N object, width and height) = (10670, 2)2.2 将未聚类前的统计结果绘图表示# 将未聚类前的统计结果绘图表示 import matplotlib.pyplot as plt plt.figure(figsize=(10,10)) plt.scatter(width_height_np[:,0],width_height_np[:,1],alpha=0.3) plt.title("Clusters",fontsize=20) plt.xlabel("normalized width",fontsize=20) plt.ylabel("normalized height",fontsize=20) plt.show()调用效果2.3 实现距离评估函数(这里用的是iou)这里iou的计算公式为:$$ \begin{array}{rl} IoU &= \frac{\textrm{intersection} }{ \textrm{union} - \textrm{intersection} }\\ \textrm{intersection} &= Min(w_1,w_2) Min(h_1,h_2)\\ \textrm{union} & = w_1 h_1 + w_2 h_2 \end{array} $$图示代码实现import numpy as np # 数据间距离评估函数 def iou(box, clusters): """ 计算一个ground truth边界盒和k个先验框(Anchor)的交并比(IOU)值。 参数box: 元组或者数据，代表ground truth的长宽。 参数clusters: 形如(k,2)的numpy数组，其中k是聚类Anchor框的个数 返回：ground truth和每个Anchor框的交并比。 """ x = np.minimum(clusters[:, 0], box[0]) y = np.minimum(clusters[:, 1], box[1]) if np.count_nonzero(x == 0) > 0 or np.count_nonzero(y == 0) > 0: raise ValueError("Box has no area") intersection = x * y box_area = box[0] * box[1] cluster_area = clusters[:, 0] * clusters[:, 1] iou_ = intersection / (box_area + cluster_area - intersection) return iou_2.4实现kmeans聚类函数# 实现kmeans聚类函数 def kmeans(boxes, k): """ 利用IOU值进行K-means聚类 参数boxes: 形状为(r, 2)的ground truth框，其中r是ground truth的个数 参数k: Anchor的个数 返回值：形状为(k, 2)的k个Anchor框 """ # 即是上面提到的r rows = boxes.shape[0] # 距离数组，计算每个ground truth和k个Anchor的距离 distances = np.empty((rows, k)) # 上一次每个ground truth"距离"最近的Anchor索引 last_clusters = np.zeros((rows,)) # 设置随机数种子 np.random.seed() # 初始化聚类中心，k个簇，从r个ground truth随机选k个 clusters = boxes[np.random.choice(rows, k, replace=False)] # 开始聚类 while True: # 计算每个ground truth和k个Anchor的距离，用1-IOU(box,anchor)来计算 for row in range(rows): distances[row] = 1 - iou(boxes[row], clusters) # 对每个ground truth，选取距离最小的那个Anchor，并存下索引 nearest_clusters = np.argmin(distances, axis=1) # 如果当前每个ground truth"距离"最近的Anchor索引和上一次一样，聚类结束 if (last_clusters == nearest_clusters).all(): break # 更新簇中心为簇里面所有的ground truth框的均值 for cluster in range(k): clusters[cluster] = np.median(boxes[nearest_clusters == cluster], axis=0) # 更新每个ground truth"距离"最近的Anchor索引 last_clusters = nearest_clusters return clusters,nearest_clusters2.4 调用测试CLUSTERS = 9 #聚类数量，anchor数量 INPUTDIM = 416 #输入网络大小 clusters_center_list,nearest_clusters = kmeans(width_height_np, k=CLUSTERS) clusters_center_list_handle = np.array(clusters_center_list)*INPUTDIM # 得到最终填入YOLOv3 的cfg文件中的anchor print('Boxes:') print(clusters_center_list_handle.astype(np.int32)) Boxes: [[ 9 37] [235 239] [ 4 30] [ 24 33] [ 5 21] [ 52 63] [ 5 26] [ 7 28] [ 6 33]]2.5聚类结果绘制与效果评估(mean_iou)查看数据聚类结果import seaborn as sns current_palette = list(sns.xkcd_rgb.values()) def plot_cluster_result(plt,clusters,nearest_clusters,mean_iou,width_height_np,k): for icluster in np.unique(nearest_clusters): pick = nearest_clusters==icluster c = current_palette[icluster] plt.rc('font', size=8) plt.plot(width_height_np[pick,0],width_height_np[pick,1],"p", color=c, alpha=0.5,label="cluster = {}, N = {:6.0f}".format(icluster,np.sum(pick))) plt.text(clusters[icluster,0], clusters[icluster,1], "c{}".format(icluster), fontsize=20,color="red") plt.title("Clusters=%d" %k) plt.xlabel("width") plt.ylabel("height") plt.legend(title="Mean IoU = {:5.4f}".format(mean_iou)) # achor结果评估 def avg_iou(boxes, clusters): """ 计算一个ground truth和k个Anchor的交并比的均值。 """ return np.mean([np.max(iou(boxes[i], clusters)) for i in range(boxes.shape[0])]) figsize = (7,5) plt.figure(figsize=figsize) mean_iou = avg_iou(width_height_np, out) plot_cluster_result(plt,clusters_center_list,nearest_clusters,mean_iou,width_height_np,k=CLUSTERS)运行效果查看聚类中心分布w = width_height_np[:, 0].tolist() h = width_height_np[:, 1].tolist() centroid_w=clusters_center_list[:,0].tolist() centroid_h=clusters_center_list[:,1].tolist() plt.figure(dpi=200) plt.title("kmeans") plt.scatter(w, h, s=10, color='b') plt.scatter(centroid_w,centroid_h,s=10,color='r') plt.show()运行效果3.汇总简略版#coding=utf-8 import xml.etree.ElementTree as ET import numpy as np import glob def iou(box, clusters): """ 计算一个ground truth边界盒和k个先验框(Anchor)的交并比(IOU)值。 参数box: 元组或者数据，代表ground truth的长宽。 参数clusters: 形如(k,2)的numpy数组，其中k是聚类Anchor框的个数 返回：ground truth和每个Anchor框的交并比。 """ x = np.minimum(clusters[:, 0], box[0]) y = np.minimum(clusters[:, 1], box[1]) if np.count_nonzero(x == 0) > 0 or np.count_nonzero(y == 0) > 0: raise ValueError("Box has no area") intersection = x * y box_area = box[0] * box[1] cluster_area = clusters[:, 0] * clusters[:, 1] iou_ = intersection / (box_area + cluster_area - intersection) return iou_ def avg_iou(boxes, clusters): """ 计算一个ground truth和k个Anchor的交并比的均值。 """ return np.mean([np.max(iou(boxes[i], clusters)) for i in range(boxes.shape[0])]) def kmeans(boxes, k): """ 利用IOU值进行K-means聚类 参数boxes: 形状为(r, 2)的ground truth框，其中r是ground truth的个数 参数k: Anchor的个数 参数dist: 距离函数 返回值：形状为(k, 2)的k个Anchor框 """ # 即是上面提到的r rows = boxes.shape[0] # 距离数组，计算每个ground truth和k个Anchor的距离 distances = np.empty((rows, k)) # 上一次每个ground truth"距离"最近的Anchor索引 last_clusters = np.zeros((rows,)) # 设置随机数种子 np.random.seed() # 初始化聚类中心，k个簇，从r个ground truth随机选k个 clusters = boxes[np.random.choice(rows, k, replace=False)] # 开始聚类 while True: # 计算每个ground truth和k个Anchor的距离，用1-IOU(box,anchor)来计算 for row in range(rows): distances[row] = 1 - iou(boxes[row], clusters) # 对每个ground truth，选取距离最小的那个Anchor，并存下索引 nearest_clusters = np.argmin(distances, axis=1) # 如果当前每个ground truth"距离"最近的Anchor索引和上一次一样，聚类结束 if (last_clusters == nearest_clusters).all(): break # 更新簇中心为簇里面所有的ground truth框的均值 for cluster in range(k): clusters[cluster] = np.median(boxes[nearest_clusters == cluster], axis=0) # 更新每个ground truth"距离"最近的Anchor索引 last_clusters = nearest_clusters return clusters # 加载自己的数据集，只需要所有labelimg标注出来的xml文件即可 def load_dataset(path): dataset = [] for xml_file in glob.glob("{}/*xml".format(path)): tree = ET.parse(xml_file) # 图片高度 height = int(tree.findtext("./size/height")) # 图片宽度 width = int(tree.findtext("./size/width")) for obj in tree.iter("object"): # 偏移量 xmin = int(obj.findtext("bndbox/xmin")) / width ymin = int(obj.findtext("bndbox/ymin")) / height xmax = int(obj.findtext("bndbox/xmax")) / width ymax = int(obj.findtext("bndbox/ymax")) / height xmin = np.float64(xmin) ymin = np.float64(ymin) xmax = np.float64(xmax) ymax = np.float64(ymax) if xmax == xmin or ymax == ymin: print(xml_file) # 将Anchor的长宽放入dateset，运行kmeans获得Anchor dataset.append([xmax - xmin, ymax - ymin]) return np.array(dataset) ANNOTATIONS_PATH = "/data/jupiter/project/dataset/209_VOC_new/Annotations" #xml文件所在文件夹 CLUSTERS = 9 #聚类数量，anchor数量 INPUTDIM = 416 #输入网络大小 data = load_dataset(ANNOTATIONS_PATH) out = kmeans(data, k=CLUSTERS) print('Boxes:') out_handle = np.array(out)*INPUTDIM print(out_handle.astype(np.int32)) print("Accuracy: {:.2f}%".format(avg_iou(data, out) * 100)) final_anchors = np.around(out[:, 0] / out[:, 1], decimals=2).tolist() print("Before Sort Ratios:\n {}".format(final_anchors)) print("After Sort Ratios:\n {}".format(sorted(final_anchors)))Boxes: [[ 8 34] [234 256] [279 239] [ 52 63] [ 6 28] [ 5 26] [ 24 33] [ 10 37] [177 216]] Accuracy: 82.93% Before Sort Ratios: [0.24, 0.92, 1.17, 0.83, 0.23, 0.19, 0.74, 0.28, 0.82] After Sort Ratios: [0.19, 0.23, 0.24, 0.28, 0.74, 0.82, 0.83, 0.92, 1.17]参考资料YOLOv3使用自己数据集——Kmeans聚类计算anchor boxes目标检测算法之YOLO系列算法的Anchor聚类
-
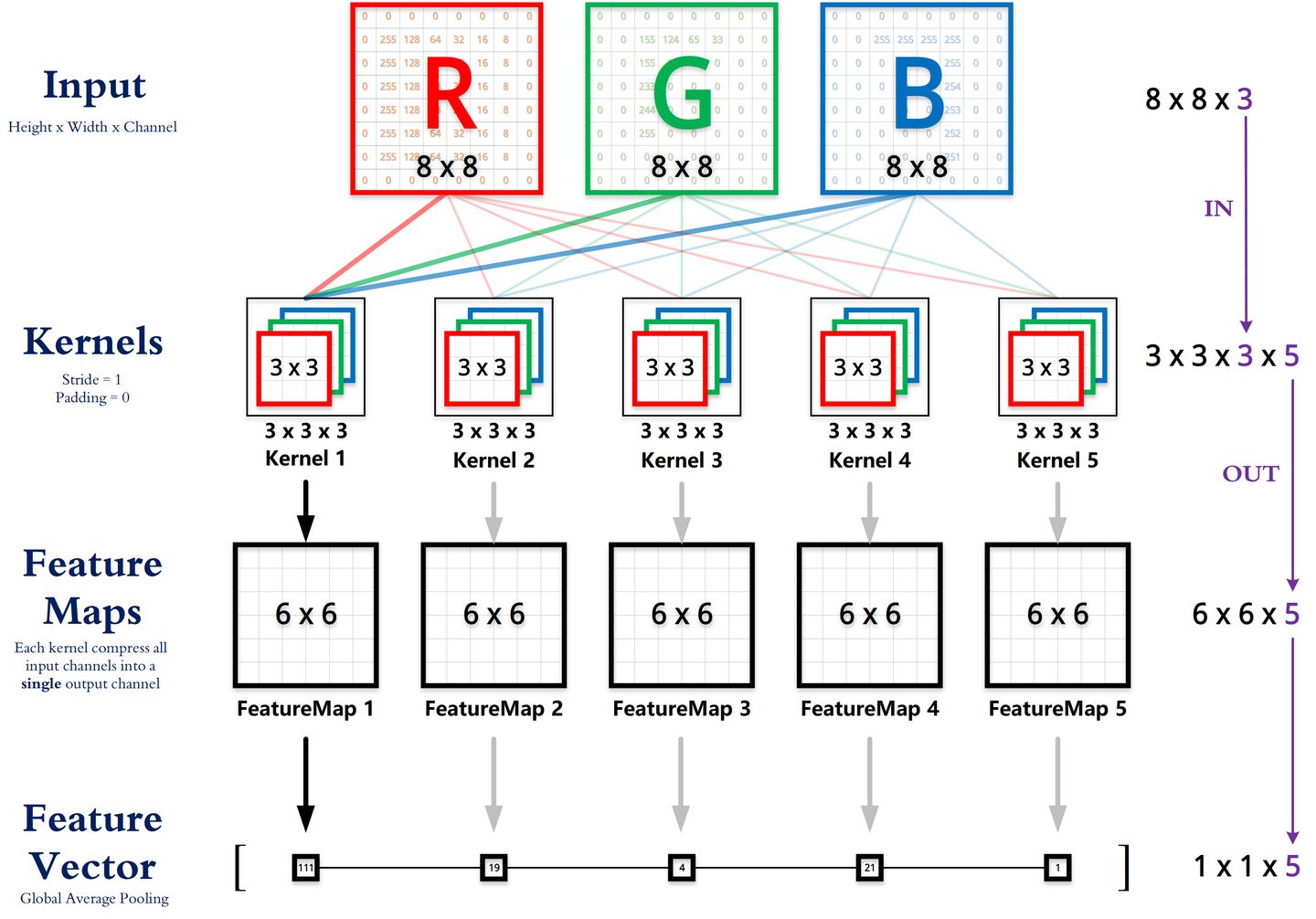
深度学习中的FLOPs介绍及计算(注意区分FLOPS) FLOPS与FLOPsFLOPS：注意全大写，是floating point operations per second的缩写，意指每秒浮点运算次数，理解为计算速度。是一个衡量硬件性能的指标。FLOPs：注意s小写，是floating point operations的缩写（s表复数），意指浮点运算数，理解为计算量。可以用来衡量算法/模型的复杂度。全连接网络中FLOPs的计算推导以4个输入神经元和3个输出神经元为例计算一个输出神经元的的计算过程为$$ y1 = w_{11}*x_1+w_{21}*x_2+w_{31}*x_3+w_{41}*x_4 $$所需的计算次数为4次乘法3次加法共需4+3=7计算。推广到I个输入神经元O个输出神经元后则计算一个输出神经元所需要的计算次数为$I+(I-1)=2I-1$，则总的计算次数为$$ FLOPs = (2I-1)*O $$考虑bias则为$$ y1 = w_{11}*x_1+w_{21}*x_2+w_{31}*x_3+w_{41}*x_4+b1 $$总的计算次数为$$ FLOPs = 2I*O $$结果FC（full connected）层FLOPs的计算公式如下(不考虑bias时有-1，有bias时没有-1):$$ FLOPs = (2 \times I - 1) \times O $$其中:I = input neuron numbers(输入神经元的数量)O = output neuron numbers(输出神经元的数量)CNN中FLOPs的计算以下答案不考虑activation function的运算推导对于输入通道数为$C_{in}$,卷积核的大小为K,输出通道数为$C_{out}$,输出特征图的尺寸为$H*W$进行一次卷积运算的计算次数为乘法$C_{in}K^2$次加法$C_{in}K^2-1$次共计$C_{in}K^2+C_{in}K^2-1=2C_{in}K^2-1$次，若考虑bias则再加1次得到一个channel的特征图所需的卷积次数为$H*W$次共计需得到$C_{out}$个特征图因此对于CNN中的一个卷积层来说总的计算次数为(不考虑bias时有-1，考虑bias时没有-1):$$ FLOPs = (2C_{in}K^2-1)HWC_{out} $$结果卷积层FLOPs的计算公式如下(不考虑bias时有-1，有bias时没有-1):$$ FLOPs = (2C_{in}K^2-1)HWC_{out} $$其中:$C_{in}$ = input channelK= kernel sizeH,W = output feature map size$C_{out}$ = output channel计算FLOPs的代码或包torchstatfrom torchstat import stat import torchvision.models as models model = models.vgg16() stat(model, (3, 224, 224)) module name input shape output shape params memory(MB) MAdd Flops MemRead(B) MemWrite(B) duration[%] MemR+W(B) 0 features.0 3 224 224 64 224 224 1792.0 12.25 173,408,256.0 89,915,392.0 609280.0 12845056.0 3.67% 13454336.0 1 features.1 64 224 224 64 224 224 0.0 12.25 3,211,264.0 3,211,264.0 12845056.0 12845056.0 1.83% 25690112.0 2 features.2 64 224 224 64 224 224 36928.0 12.25 3,699,376,128.0 1,852,899,328.0 12992768.0 12845056.0 8.43% 25837824.0 3 features.3 64 224 224 64 224 224 0.0 12.25 3,211,264.0 3,211,264.0 12845056.0 12845056.0 1.45% 25690112.0 4 features.4 64 224 224 64 112 112 0.0 3.06 2,408,448.0 3,211,264.0 12845056.0 3211264.0 11.37% 16056320.0 5 features.5 64 112 112 128 112 112 73856.0 6.12 1,849,688,064.0 926,449,664.0 3506688.0 6422528.0 4.03% 9929216.0 6 features.6 128 112 112 128 112 112 0.0 6.12 1,605,632.0 1,605,632.0 6422528.0 6422528.0 0.73% 12845056.0 7 features.7 128 112 112 128 112 112 147584.0 6.12 3,699,376,128.0 1,851,293,696.0 7012864.0 6422528.0 5.86% 13435392.0 8 features.8 128 112 112 128 112 112 0.0 6.12 1,605,632.0 1,605,632.0 6422528.0 6422528.0 0.37% 12845056.0 9 features.9 128 112 112 128 56 56 0.0 1.53 1,204,224.0 1,605,632.0 6422528.0 1605632.0 7.32% 8028160.0 10 features.10 128 56 56 256 56 56 295168.0 3.06 1,849,688,064.0 925,646,848.0 2786304.0 3211264.0 3.30% 5997568.0 11 features.11 256 56 56 256 56 56 0.0 3.06 802,816.0 802,816.0 3211264.0 3211264.0 0.00% 6422528.0 12 features.12 256 56 56 256 56 56 590080.0 3.06 3,699,376,128.0 1,850,490,880.0 5571584.0 3211264.0 5.13% 8782848.0 13 features.13 256 56 56 256 56 56 0.0 3.06 802,816.0 802,816.0 3211264.0 3211264.0 0.37% 6422528.0 14 features.14 256 56 56 256 56 56 590080.0 3.06 3,699,376,128.0 1,850,490,880.0 5571584.0 3211264.0 4.76% 8782848.0 15 features.15 256 56 56 256 56 56 0.0 3.06 802,816.0 802,816.0 3211264.0 3211264.0 0.37% 6422528.0 16 features.16 256 56 56 256 28 28 0.0 0.77 602,112.0 802,816.0 3211264.0 802816.0 2.56% 4014080.0 17 features.17 256 28 28 512 28 28 1180160.0 1.53 1,849,688,064.0 925,245,440.0 5523456.0 1605632.0 3.66% 7129088.0 18 features.18 512 28 28 512 28 28 0.0 1.53 401,408.0 401,408.0 1605632.0 1605632.0 0.00% 3211264.0 19 features.19 512 28 28 512 28 28 2359808.0 1.53 3,699,376,128.0 1,850,089,472.0 11044864.0 1605632.0 5.50% 12650496.0 20 features.20 512 28 28 512 28 28 0.0 1.53 401,408.0 401,408.0 1605632.0 1605632.0 0.00% 3211264.0 21 features.21 512 28 28 512 28 28 2359808.0 1.53 3,699,376,128.0 1,850,089,472.0 11044864.0 1605632.0 5.49% 12650496.0 22 features.22 512 28 28 512 28 28 0.0 1.53 401,408.0 401,408.0 1605632.0 1605632.0 0.00% 3211264.0 23 features.23 512 28 28 512 14 14 0.0 0.38 301,056.0 401,408.0 1605632.0 401408.0 1.10% 2007040.0 24 features.24 512 14 14 512 14 14 2359808.0 0.38 924,844,032.0 462,522,368.0 9840640.0 401408.0 2.94% 10242048.0 25 features.25 512 14 14 512 14 14 0.0 0.38 100,352.0 100,352.0 401408.0 401408.0 0.00% 802816.0 26 features.26 512 14 14 512 14 14 2359808.0 0.38 924,844,032.0 462,522,368.0 9840640.0 401408.0 2.57% 10242048.0 27 features.27 512 14 14 512 14 14 0.0 0.38 100,352.0 100,352.0 401408.0 401408.0 0.00% 802816.0 28 features.28 512 14 14 512 14 14 2359808.0 0.38 924,844,032.0 462,522,368.0 9840640.0 401408.0 2.19% 10242048.0 29 features.29 512 14 14 512 14 14 0.0 0.38 100,352.0 100,352.0 401408.0 401408.0 0.37% 802816.0 30 features.30 512 14 14 512 7 7 0.0 0.10 75,264.0 100,352.0 401408.0 100352.0 0.37% 501760.0 31 avgpool 512 7 7 512 7 7 0.0 0.10 0.0 0.0 0.0 0.0 0.00% 0.0 32 classifier.0 25088 4096 102764544.0 0.02 205,516,800.0 102,760,448.0 411158528.0 16384.0 10.62% 411174912.0 33 classifier.1 4096 4096 0.0 0.02 4,096.0 4,096.0 16384.0 16384.0 0.00% 32768.0 34 classifier.2 4096 4096 0.0 0.02 0.0 0.0 0.0 0.0 0.37% 0.0 35 classifier.3 4096 4096 16781312.0 0.02 33,550,336.0 16,777,216.0 67141632.0 16384.0 2.20% 67158016.0 36 classifier.4 4096 4096 0.0 0.02 4,096.0 4,096.0 16384.0 16384.0 0.00% 32768.0 37 classifier.5 4096 4096 0.0 0.02 0.0 0.0 0.0 0.0 0.37% 0.0 38 classifier.6 4096 1000 4097000.0 0.00 8,191,000.0 4,096,000.0 16404384.0 4000.0 0.73% 16408384.0 total 138357544.0 109.39 30,958,666,264.0 15,503,489,024.0 16404384.0 4000.0 100.00% 783170624.0 ============================================================================================================================================================ Total params: 138,357,544 ------------------------------------------------------------------------------------------------------------------------------------------------------------ Total memory: 109.39MB Total MAdd: 30.96GMAdd Total Flops: 15.5GFlops Total MemR+W: 746.89MB 参考资料CNN 模型所需的计算力（flops）和参数（parameters）数量是怎么计算的？分享一个FLOPs计算神器CNN Explainer[Molchanov P , Tyree S , Karras T , et al. Pruning Convolutional Neural Networks for Resource Efficient Transfer Learning[J]. 2016.](https://arxiv.org/pdf/1611.06440.pdf)
-
机器学习——几种距离度量方法 机器学习——几种距离度量方法1. 欧氏距离(Euclidean Distance)欧氏距离是最容易直观理解的距离度量方法，我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。二维平面上点a(x1,y1)与b(x2,y2)间的欧氏距离:三维空间点a(x1,y1,z1)与b(x2,y2,z2)间的欧氏距离:n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)间的欧氏距离（两个n维向量）：2. 曼哈顿距离(Manhattan Distance)顾名思义，在曼哈顿街区要从一个十字路口开车到另一个十字路口，驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”(City Block distance)。二维平面两点a(x1,y1)与b(x2,y2)间的曼哈顿距离：n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的曼哈顿距离：3. 切比雪夫距离 (Chebyshev Distance)国际象棋中，国王可以直行、横行、斜行，所以国王走一步可以移动到相邻8个方格中的任意一个。国王从格子(x1,y1)走到格子(x2,y2)最少需要多少步？这个距离就叫切比雪夫距离。二维平面两点a(x1,y1)与b(x2,y2)间的切比雪夫距离：n维空间点a(x11,x12,…,x1n)与b(x21,x22,…,x2n)的切比雪夫距离：4.标准化欧氏距离 (Standardized Euclidean Distance)定义： 标准化欧氏距离是针对欧氏距离的缺点而作的一种改进。标准欧氏距离的思路：既然数据各维分量的分布不一样，那先将各个分量都“标准化”到均值、方差相等。假设样本集X的均值(mean)为m，标准差(standard deviation)为s，X的“标准化变量”表示为：标准化欧氏距离公式：如果将方差的倒数看成一个权重，也可称之为加权欧氏距离(Weighted Euclidean distance)。5 余弦距离(Cosine Distance)几何中，夹角余弦可用来衡量两个向量方向的差异；机器学习中，借用这一概念来衡量样本向量之间的差异。二维空间中向量A(x1,y1)与向量B(x2,y2)的夹角余弦公式：两个n维样本点a(x11,x12,…,x1n)和b(x21,x22,…,x2n)的夹角余弦为：即：夹角余弦取值范围为[-1,1]。余弦越大表示两个向量的夹角越小，余弦越小表示两向量的夹角越大。当两个向量的方向重合时余弦取最大值1，当两个向量的方向完全相反余弦取最小值-1。参考资料机器学习——几种距离度量方法比较：https://my.oschina.net/hunglish/blog/787596
-
Kmeans算法简介 Kmeans算法简介算法介绍人的“物以类聚”新生入学后根据各自的喜好加入对应的社团。数据的“物以类聚”如果把人类比机器学习中的数据，那么聚类就很好理解了每当这个类别中有了新的数据加入的时候，我们要做的就是更新这个类别的中心位置，以方便这个新样本去适应这个类别，这便是kmeans算法的主要逻辑了。如何定义相似用两个点的距离：如欧式距离引入cluster的相关概念Kmean聚类实例处理步骤：随机从数据集中选取K个样本当做centroid对于数据集中的每个点，计算它距离每个centroid的距离，并把它归为距离最近的那个cluster更新新的centroid位置重复2.3，直到centroid的位置不再改变KMEANS的优缺点优点非监督类的算法不需要样本的标注信息缺点不能利用到数据的标注信息，意味着模型的性能不如其他监督学习对于K的取值，也就是你认为数据集中的样本应该分为几类，这个参数的设置极为敏感！对于数据集本身样本的分布也很敏感参考资料【五分钟机器学习】物以类聚的Kmeans：https://www.bilibili.com/video/BV1ei4y1V7hX?from=search&seid=12931680004886943436
-
