ShuffleNet-v2简介与实现

1.原论文

ECCV2018--ShuffleNet V2: Practical Guidelines for Efficient CNN Architecture Design

2.设计理念

目前衡量模型复杂度的一个通用指标是FLOPs，具体指的是multiply-add数量，但是这却是一个间接指标，因为它不完全等同于速度。如图1中的（c）和（d）

图1：ShuffleNetv2与其它算法在不同平台下的复杂度、速度以及准确度对比

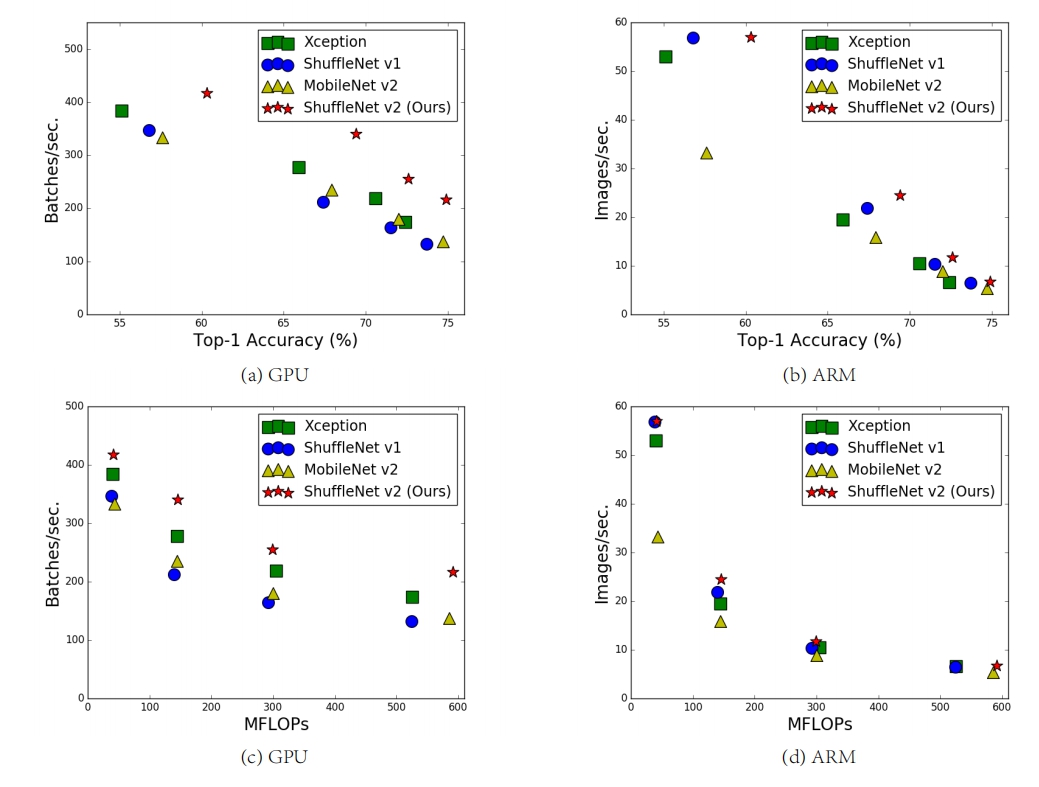
可以看到相同FLOPs的两个模型，其速度却存在差异。这种不一致主要归结为两个原因，首先影响速度的不仅仅是FLOPs，如内存使用量（memory access cost, MAC），这不能忽略，对于GPUs来说可能会是瓶颈。另外模型的并行程度也影响速度，并行度高的模型速度相对更快。另外一个原因，模型在不同平台上的运行速度是有差异的，如GPU和ARM，而且采用不同的库也会有影响。

3.根据设计理念及实验得出的4条基本设计准则

3.1探索实验

据此，作者在特定的平台下研究ShuffleNetv1和MobileNetv2的运行时间，并结合理论与实验得到了4条实用的指导原则：

G1:同等通道大小最小化内存访问量

对于轻量级CNN网络，常采用深度可分割卷积（depthwise separable convolutions），其中点卷积（ pointwise convolution）即1x1卷积复杂度最大。这里假定输入和输出特征的通道数分别为 $c1$和$c2$，特征图的空间大小为$h \times w$，那么1x1卷积的FLOPs为

$$ B=hwc_1c_2 $$

对应的MAC(memory access cost)为

$$ MAC = hw(c_1+c_2)+c_1c_2 $$

根据均值不等式（这里假定内存足够），固定B时，MAC存在下限（令$c_2=\frac{B}{hwc_1}$），则

$$ MAC \ge 2 \sqrt{hwB} + \frac{B}{hw} $$

仅当$c_1=c_2$时，MAC取最小值，这个理论分析也通过实验得到证实，如下表所示，通道比为1:1时速度更快。

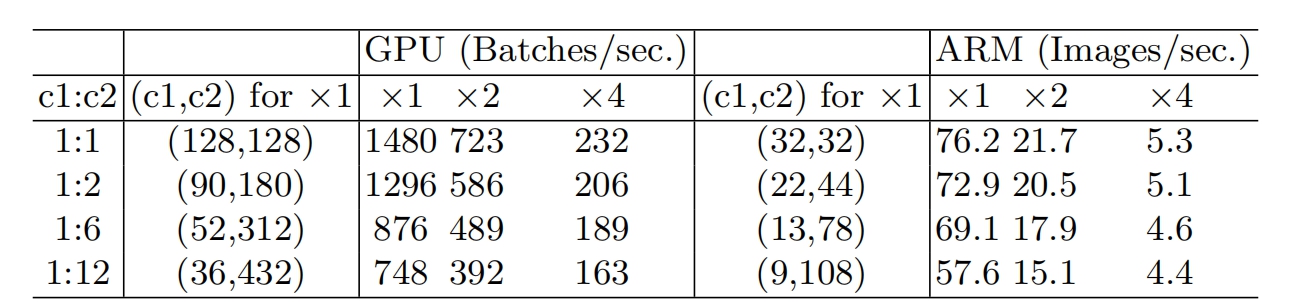
G2:过量使用组卷积会增加MAC(memory access cost)

组卷积（group convolution）是常用的设计组件，因为它可以减少复杂度却不损失模型容量。但是这里发现，分组过多会增加MAC(memory access cost)。对于组卷积，FLOPs为(其中g为组数)：

$$ B = hwc_1c_2/g $$

对应的MAC(memory access cost)为

$$ MAC = hwc_1+Bg/c_1+B/hw $$

可以看到，在输入确定，B相同时，当g增加时,MAC(memory access cost)会同时增加，下表是对应的实验，所以明智之举是不要使用太大 ![[公式]](https://www.zhihu.com/equation?tex=g) 的组卷积。

G3:网络碎片化会降低并行度

一些网络如Inception，以及Auto ML自动产生的网络NASNET-A，它们倾向于采用“多路”结构，即存在一个lock中很多不同的小卷积或者pooling，这很容易造成网络碎片化，减低模型的并行度，相应速度会慢，这也可以通过实验得到证明。

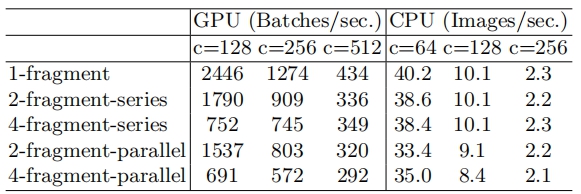
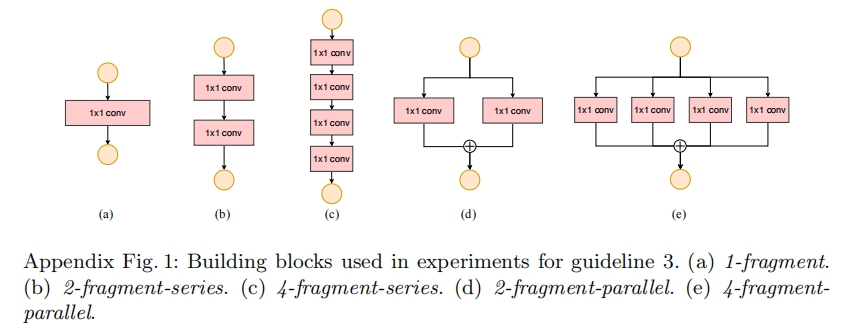
G4:不能忽略元素级操作(比如ReLU和Add)

对于元素级（element-wise operators）比如ReLU和Add，虽然它们的FLOPs较小，但是却需要较大的MAC(memory access cost)。这里实验发现如果将ResNet中残差单元中的ReLU和shortcut移除的话，速度有20%的提升。

4.ShuffleNet-v1 基本结构及存在的问题

4.1ShuffleNet-v1基本结构

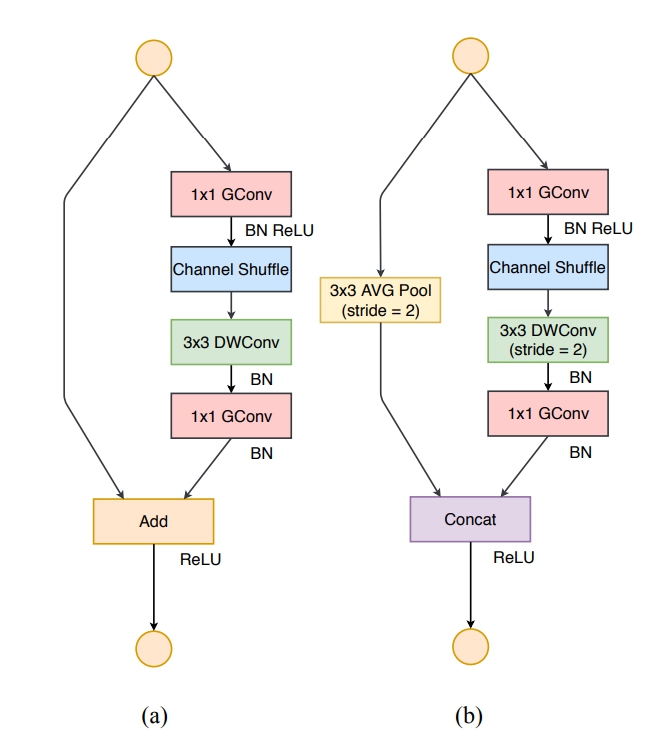
其中:

(a) the basic ShufflleNet unit;
(b) the ShufflleNet unit for spatial down sampling (2×);

4.2ShuffleNet-v1存在的问题

在ShuffleNetv1的模块中，大量使用了1x1组卷积，这违背了G2原则，
另外v1采用了类似ResNet中的瓶颈层（bottleneck layer），输入和输出通道数不同，这违背了G1原则。
同时使用过多的组，也违背了G3原则。
短路连接中存在大量的元素级Add运算，这违背了G4原则。

5.ShuffleNet-v2基本块及改进分析

5.1ShuffleNet-v2基本块

根据前面的4条准则，作者分析了ShuffleNetv1设计的不足，并在此基础上改进得到了ShuffleNetv2，两者模块上的对比如下图所示：

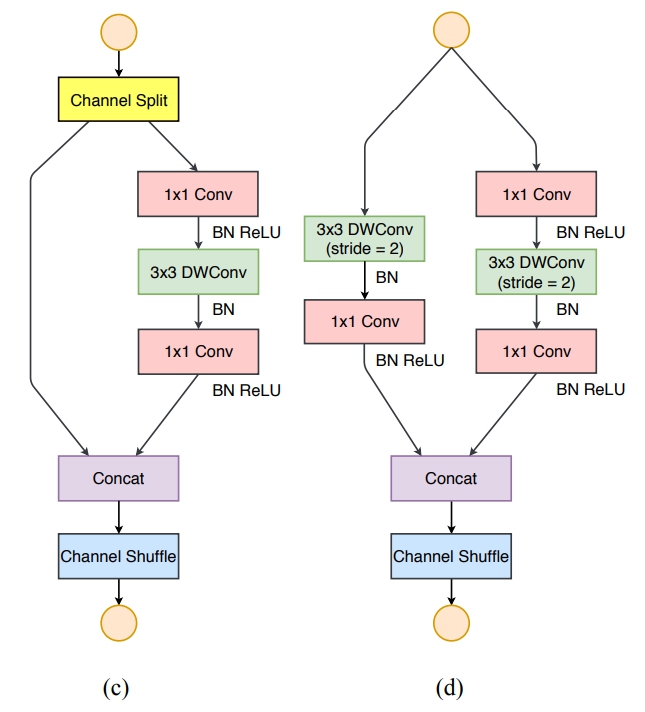
其中

(c) the basic ShufflleNetv2 unit;
(d) the ShufflleNetv2 unit for spatial down sampling (2×);
DWConv: depthwise convolution
GConv:group convolution

对于ShufflleNetv2基本块(the ShufflleNetv2 unit)还可以选择是否采用SE(Squeeze-and-Excitation)模块和残差(residual)结构

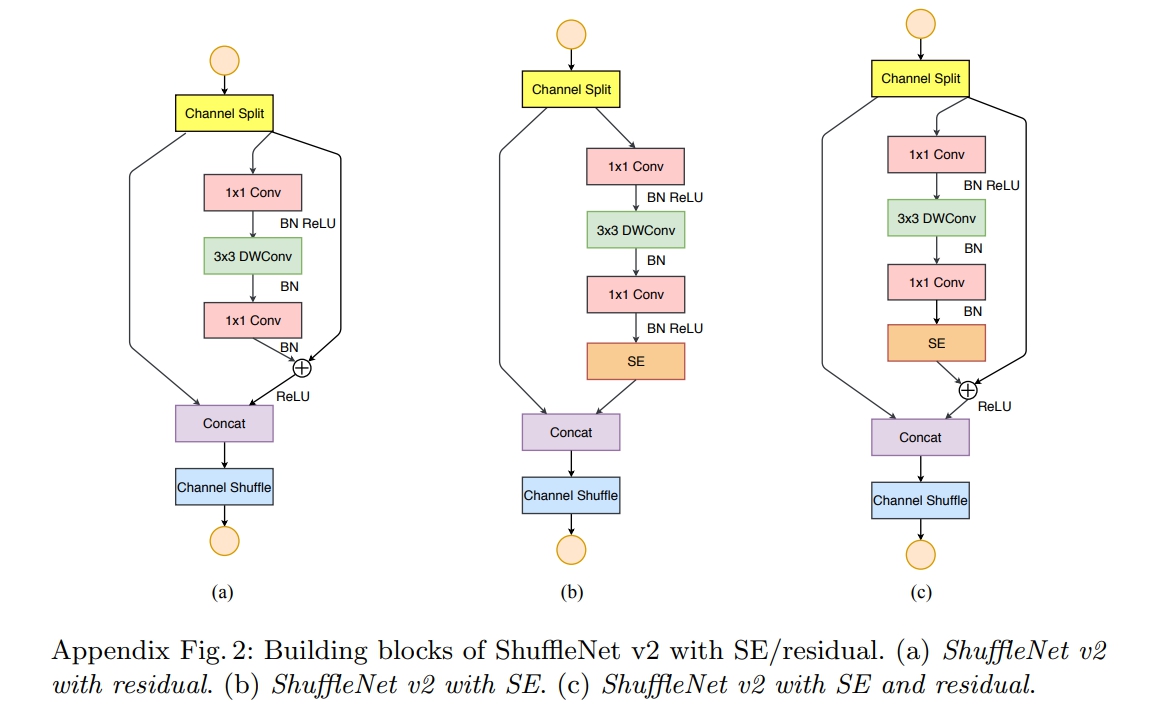
5.2ShuffleNetv2的改进分析

为了改善v1的缺陷，根据四条原则，作者提出了shufflenet v2。v2版本引入了一种新的运算：channel split（如上图网路结构中的图c）。

channel split的做法：

在开始时先将输入特征图在通道维度分成两个分支：通道数分别为 $c'$ 和 $c-c'$ ，实际实现时$c'=c/2$ 。
一个是identity，一个经过三个conv，然后concat到一起，这个满足G4。
右边的分支包含3个连续的卷积，并且输入和输出通道相同，这符合G1。
而且两个1x1卷积不再是组卷积，这符合G2
另外两个分支相当于已经分成两组。两个分支的输出不再是Add元素，而是concat在一起。
取替了element-wise操作add。最后经过channel shuffle将两个分支的信息进行交流。

channel split的作用：

第一，划分一半到右分支，意味着右边计算量减少，从而可以提高channel数，提高网络capacity。
第二，左分支相当于一种特征重用(feature reuse), 跟DenseNet和CondenseNet一样的思想。

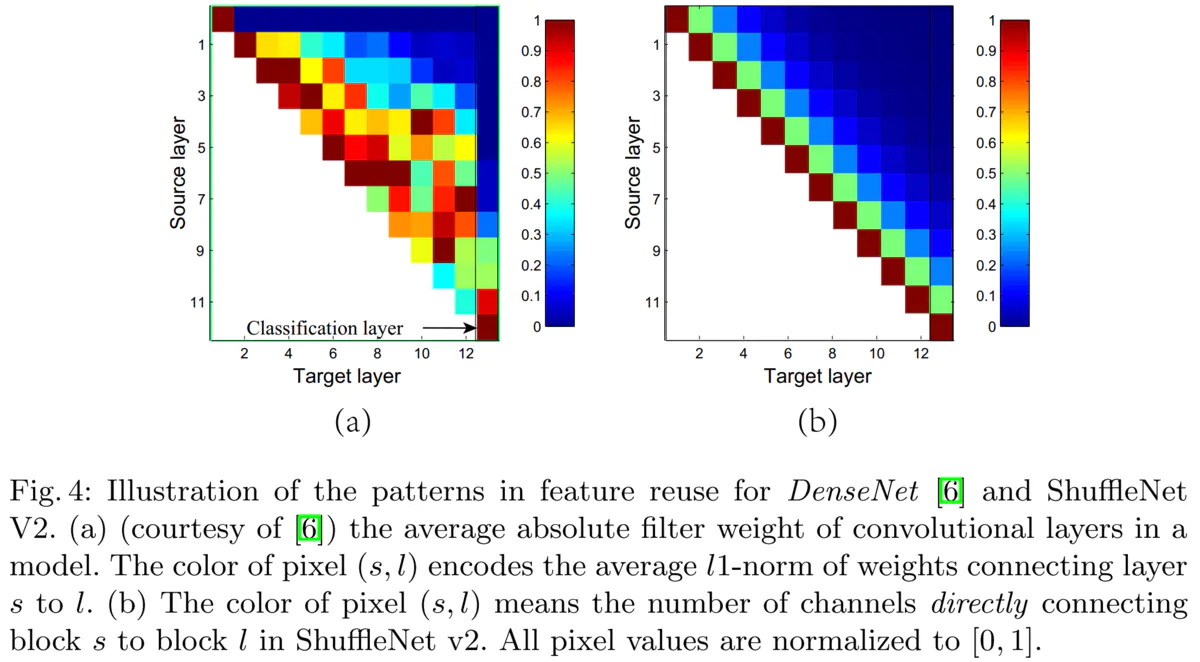
下图(a)为DenseNet的从source layer到target layer连接的权重的大小，可见target层前1-3层的信息对当前层帮助较大，而越远的连接比较多余。图(b)为ShuffleNet v2的情况，
因为shuffle操作会导致每次会有一半的channel到下一层。因此，作者认为shufflenet跟densenet一样的利用到了feature reuse，所以有效。

6.ShuffleNet-v2完整网络结构

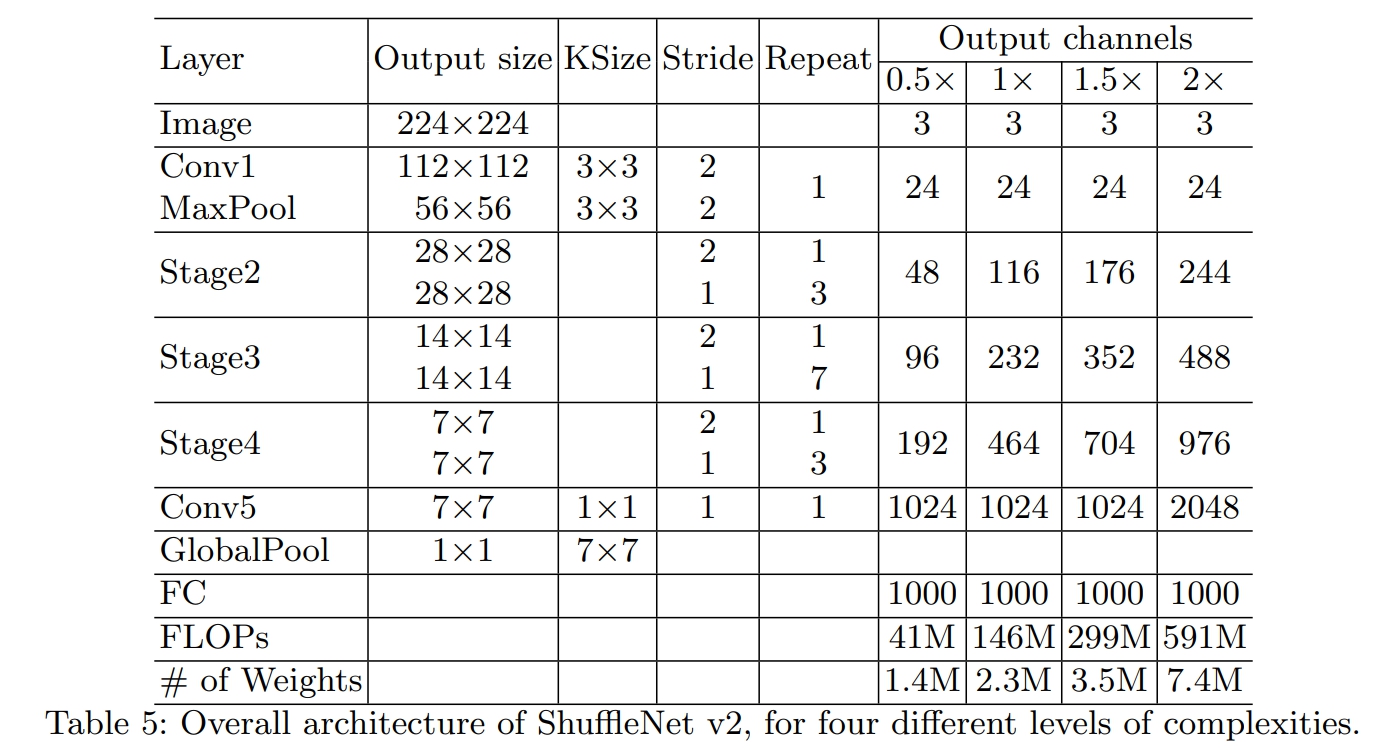
其中：

1个stage=1个DSampling+Repeat个BasicUnit

7.ShuffleNet-v2基本块实现(pytorch)

7.1Channel Shuffle

图示

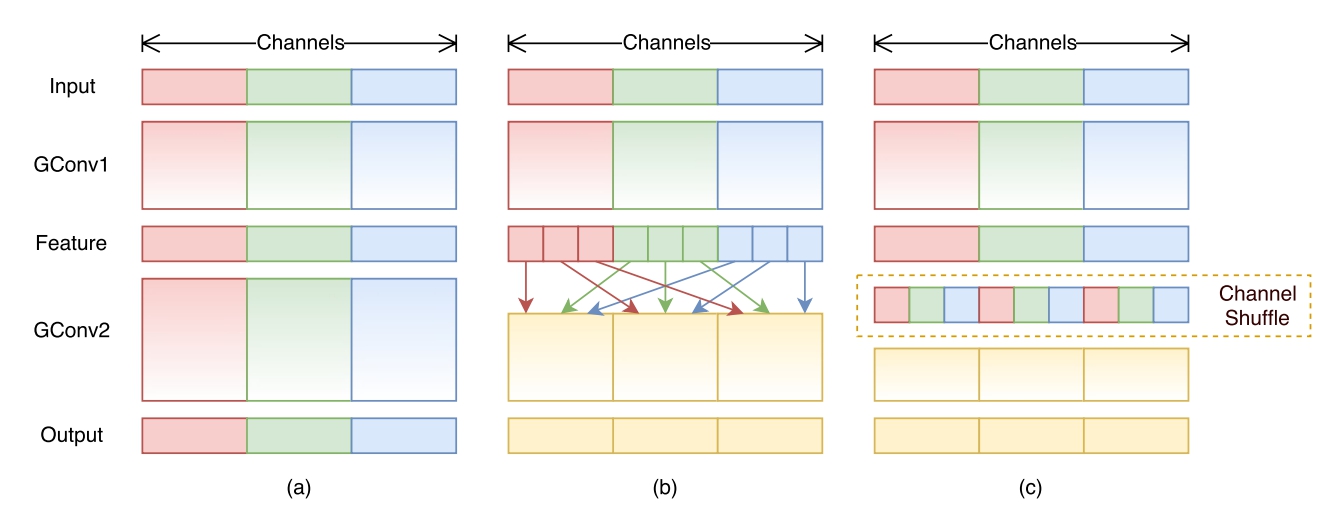
实现步骤
- 假定将输入层分为 g 组，总通道数为 g × n 。
- 首先你将通道那个维度拆分为 (g,n) 两个维度
- 然后将这两个维度转置变成 (n,g)
- 最后重新reshape成一个维度 g × n 。
代码

#  Channel Shuffle
def shuffle_chnls(x, groups=2):
    """Channel Shuffle"""

    bs, chnls, h, w = x.data.size()
    
    # 如果通道数不是分组的整数被，则无法进行Channel Shuffle操作，直接返回x
    if chnls % groups:
        return x
     
    # 计算用于Channel Shuffle的一个group的的通道数
    chnls_per_group = chnls // groups
    
    # 执行channel shuffle操作
    x = x.view(bs, groups, chnls_per_group, h, w) # 将通道那个维度拆分为 (g,n) 两个维度
    x = torch.transpose(x, 1, 2).contiguous() # 将这两个维度转置变成 (n,g)
    x = x.view(bs, -1, h, w) # 最后重新reshape成一个维度 g × n g\times ng×n
    
    return x

7.2ShufflleNetv2基本块( the basic ShufflleNetv2 unit)

基本结构图示

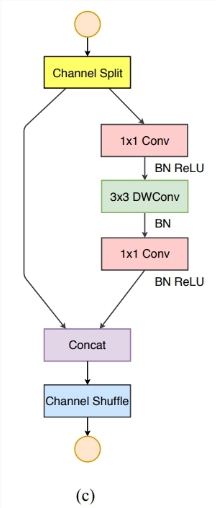
增加SE(Squeeze-and-Excitation)模块和残差(residual)结构后的基本块结构图示

代码

#  封装一个Conv+BN+RELU的基本块
class BN_Conv2d(nn.Module):
    def __init__(self, in_channels, out_channels, kernel_size, stride, padding,
                 dilation=1, groups=1, bias=False, activation=True): # dilation=1-->卷积核膨胀
        super(BN_Conv2d, self).__init__()
        layers = [nn.Conv2d(in_channels, out_channels, kernel_size=kernel_size, stride=stride,
                            padding=padding, dilation=dilation, groups=groups, bias=bias),
                  nn.BatchNorm2d(out_channels)]
        if activation:
            layers.append(nn.ReLU(inplace=True))
        self.seq = nn.Sequential(*layers)

    def forward(self, x):
        return self.seq(x)

# ShuffleNet-v2基本块
class BasicUnit(nn.Module):
    def __init__(self, in_chnls, out_chnls, is_se=False, is_residual=False, c_ratio=0.5, groups=2):
        super(BasicUnit, self).__init__()
        self.is_se, self.is_res = is_se, is_residual # 是否使用SE结构和残差结构
        self.l_chnls = int(in_chnls * c_ratio) # 左侧输入通道数
        self.r_chnls = in_chnls - self.l_chnls # 右侧输入通道数
        self.ro_chnls = out_chnls - self.l_chnls # 右侧输出通道数
        self.groups = groups 

        # layers
        self.conv1 = BN_Conv2d(self.r_chnls, self.ro_chnls, 1, 1, 0)
        self.dwconv2 = BN_Conv2d(self.ro_chnls, self.ro_chnls, 3, 1, 1,  # same padding, depthwise conv
                                 groups=self.ro_chnls, activation=None)
        act = False if self.is_res else True
        self.conv3 = BN_Conv2d(self.ro_chnls, self.ro_chnls, 1, 1, 0, activation=act)
        
        # 是否使用SE模块和residual结构
        if self.is_se: 
            self.se = SE(self.ro_chnls, 16)
        if self.is_res: 
            self.shortcut = nn.Sequential()
            if self.r_chnls != self.ro_chnls:
                self.shortcut = BN_Conv2d(self.r_chnls, self.ro_chnls, 1, 1, 0, activation=False)

    def forward(self, x):
        # channel split 操作
        x_l = x[:, :self.l_chnls, :, :]
        x_r = x[:, self.r_chnls:, :, :]

        # right path
        out_r = self.conv1(x_r)
        out_r = self.dwconv2(out_r)
        out_r = self.conv3(out_r)
        
        # 是否使用SE模块和residual结构
        if self.is_se:
            coefficient = self.se(out_r)
            out_r *= coefficient
        if self.is_res:
            out_r += self.shortcut(x_r)

        # concatenate
        out = torch.cat((x_l, out_r), 1)
        return shuffle_chnls(out, self.groups)

7.3ShufflleNetv2下采样基本块(the ShufflleNetv2 unit for spatial down sampling)

图示

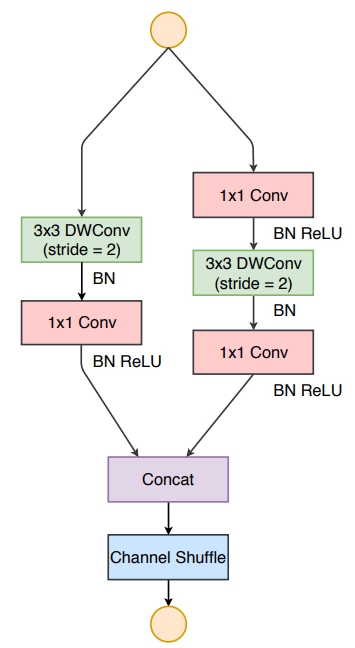
代码

# SuffleNet-v2下采样基本块
class DSampling(nn.Module):
    def __init__(self, in_chnls, groups=2):
        super(DSampling, self).__init__()
        self.groups = groups
        # down-sampling(通过stride=2实现), depth-wise conv(通过groups=in_chnls实现).
        self.dwconv_l1 = BN_Conv2d(in_chnls, in_chnls, 3, 2, 1,  
                                   groups=in_chnls, activation=None)
        self.conv_l2 = BN_Conv2d(in_chnls, in_chnls, 1, 1, 0)
        self.conv_r1 = BN_Conv2d(in_chnls, in_chnls, 1, 1, 0)
        self.dwconv_r2 = BN_Conv2d(in_chnls, in_chnls, 3, 2, 1, groups=in_chnls, activation=False)
        self.conv_r3 = BN_Conv2d(in_chnls, in_chnls, 1, 1, 0)

    def forward(self, x):
        # left path
        out_l = self.dwconv_l1(x)
        out_l = self.conv_l2(out_l)

        # right path
        out_r = self.conv_r1(x)
        out_r = self.dwconv_r2(out_r)
        out_r = self.conv_r3(out_r)

        # concatenate
        out = torch.cat((out_l, out_r), 1)
        return shuffle_chnls(out, self.groups)

8.ShuffleNet-v2网络结构实现

# TODO